When the basic parabola y = x2 is reflected in the x axis, the point (3, 9), for example, is reflected to the point (3, 9) Indeed the general point (a, a2) becomes (a, − a2) and so the equation satisfied by these points is y = −x2 We can confirm this with a table of valuesA parabola is symmetric about the vertexThis video solution is related to the Ontario highschool textbook 10 Principles of Mathematics Nelson

Parabola Parent Function Mathbitsnotebook A1 Ccss Math
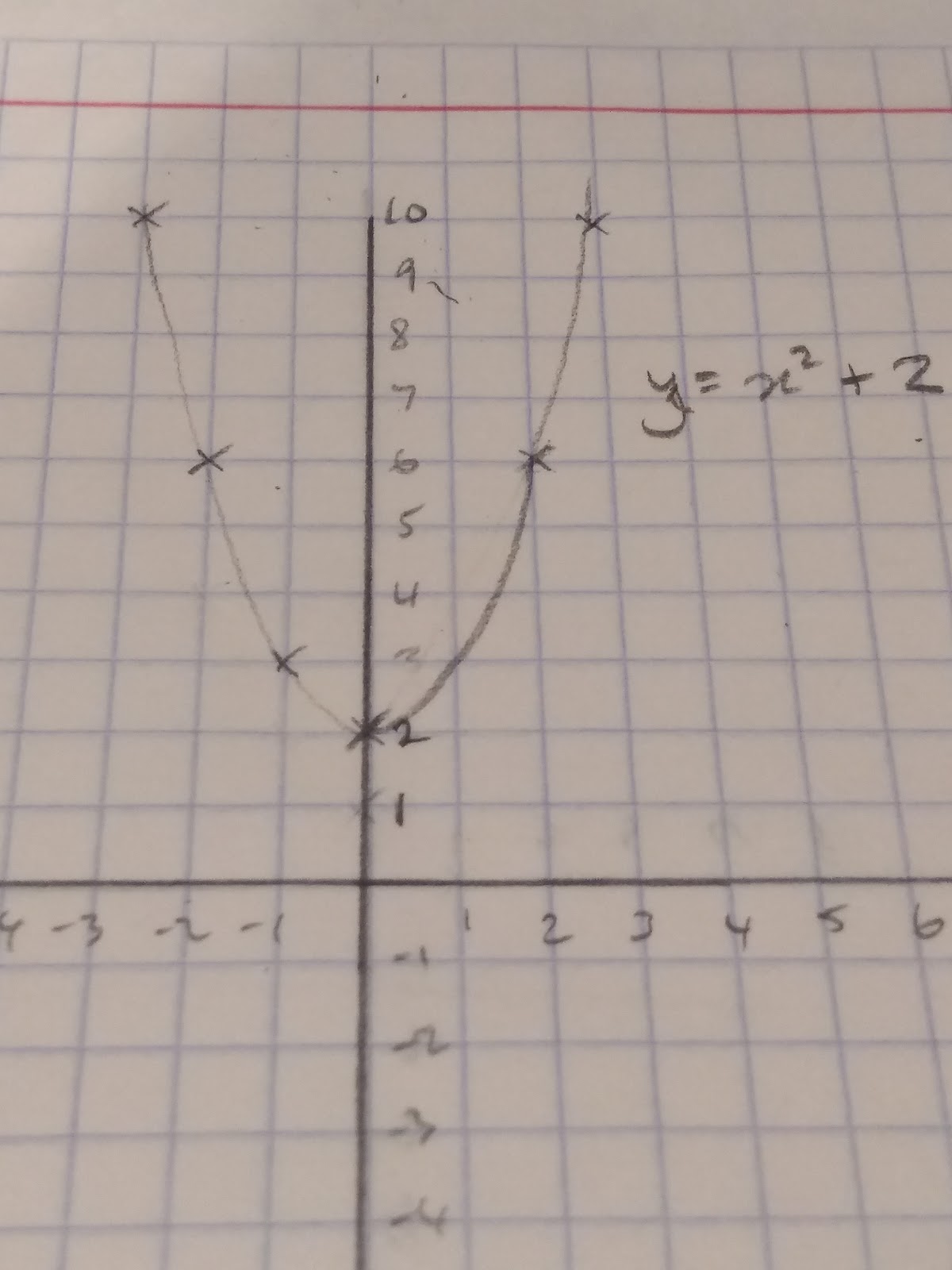
Parabola congruent to y=x^2
Parabola congruent to y=x^2-Consider a parabola P that is congruent to y=x 2, opens upward and has a vertex of (1,3) Now find the equation of the new parabola that results it P is reflected in the xConsider a parabola P that is congruent to y = x 2, opens upward, and has vertex (–1, 3) Now find the equation of a new parabola that results if p is reflected in the x–axis and translated 3 units down




Attributes Of Quadratic Flashcards Quizlet
Math Consider a parabola P that is congruent (has the same shape) to y=x^2, opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left_Mpm2dc all of unit 4markeddocx Mpm2dc all of unit 4 Your mark for this unit is 735\/87 = 84 Mpm2dc unit 41 14\/18 41 a The parabola definedThe graph is the part of a parabola, congruent to y ˜ x2, with vertex (3, 4), for which x #3 From the graph, the range is y #4 ©P DO NOT COPY 45 Inverse Relations 265 14 A graph was reflected in the line y = x Its reflection image is shown Determine an
Safety How works Test new features Press Copyright Contact us Creators14 A parabola is congruent to y x 2 2 and passes through (2, 2) and (5, 4) Determine its equation in vertex and standard form 15 The height of a ball thrown up in the air is given ash t t 49 294 12 Determine the maximum height reached by the ball and how long it took to get there4 5a) 2 marks b) the parabola opens upwards and is stretched vertically by a factor of 5
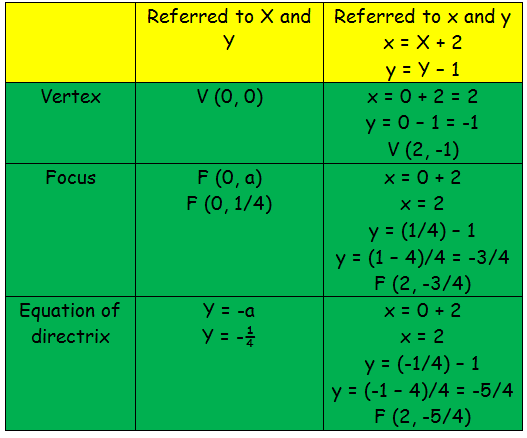
6 The idea is to look at a single parabola of the form y = x 2 r, and determine r such that the parabola is tangent to the lines y = ±Write the equation with y 0 on one side y 0 = x 0 2 4 − x 0 5 This equation in ( x 0, y 0) is true for all other values on the parabola and hence we can rewrite with ( x, y) So, the equation of the parabola with focus ( 2, 5) and directrix is y = 3 is y = x 2 4 − x 5Parabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the



Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 360 parabolas and properties packet Pdf



1
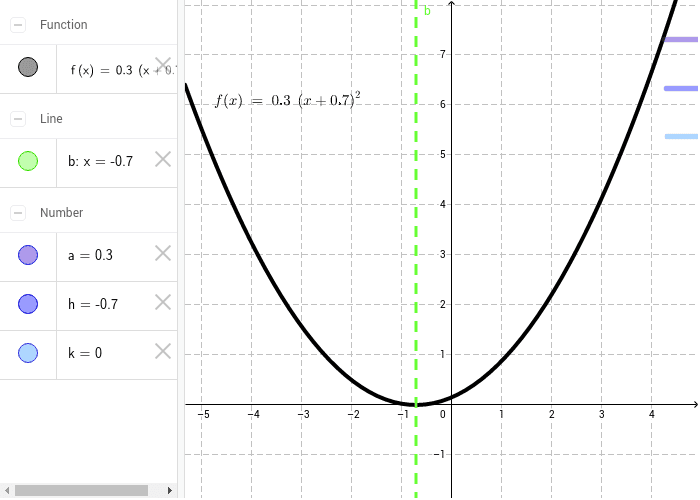
= –4ay Since the parabola passesNew parabola should be congruent (the same shape and size) to y = x2, with the same vertex, except it should open downward so its vertex will be its highest point Record the Find a way to change the equation to make the y = x2 parabola move 3 units to the left and stretch vertically, as in part (c)Your new parabola might look like y = 4x2We're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0




Content Transformations Of The Parabola




Solved Hand 9 Write The Equation For Each Parabola With Chegg Com
Write an equation of a parabola that satisfies each set of conditions a) opens upward, congruent to y=x^2and vertex (0, 4) b) opens upward, congruent to y=x^2Every parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equationParabolas can have both xintercepts and y intercepts yintercept As you can see from the picture below, the yintercept is the point at which the parabola intercepts the yaxis xintercepts The xintercepts are the points or the point at which the parabola intersects the xaxis A parabola can have either 2,1 or zero real x intercepts



How To Find Focus Directrix And Vertex Of Parabola



Transformations To The Graph Of Y X 2 Geogebra
A hyperbolic paraboloid (not to be confused with a hyperboloid) is a doubly ruled surface shaped like a saddleIn a suitable coordinate system, a hyperbolic paraboloid can be represented by the equation 6 = In this position, the hyperbolic paraboloid opens downward along the xaxis and upward along the yaxis (that is, the parabola in the plane x = 0 opens upward and the parabola(x2 2)2 1 All 4 parabolas are congruent to y x2, and have vertex (0, 4) The equation is y x2 4 The curve is solid and The curve is broken and the the shaded region is below shaded region is above An inequality is y x2 4 An inequality is y>x2 4 The curve is solid0 up (0,0) x 0 Yes y x2 2 y x2 4 y x2 1 y x2 and y ax2 Clear all previous equations from your calculator Repeat part A for the following




Resourceaholic Tricks And Tips 3 Quadratics



Parabola Knowino
The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3) Observe the graph of yFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceGraphing Parabolas Part 4 Graphing Recap Graphing by Completing the Square Intro Graphing by Completing the Square How Graphing by Completing the Square Freaky Things That Can Happen Making the Connection Between Graphing and Solving Coolmath privacy policy



Solution Can You Help Me With This Problem A Parabola Is Congruent To Y X 2 And Has X Intercepts 1 And 5 Determine The Coordinates Of The Vertex



Quadratic Function
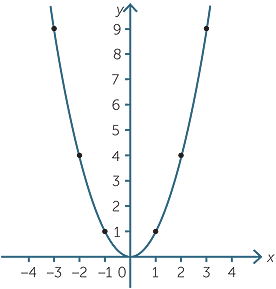
#y=x^2# is the Parent Function for a quadratic equation The graph of #y=x^2# is useful in understanding the behavior of the function given #color(red)(y = 4x^2# Since, the sign of the #x^2# term is positive, the parabola opens up and we have a Minimum point at the Vertex #color(green)(Step 2 # Plot the Points from the data table to drawQuestion Write an equation for a parabola that is congruent to the graph of y = x 2, opens downward, and has its vertex at (3,1) check_circle2 Given y = 3x2 1) Write the equation of a parabola that contains the point (2, 12) that is congruent to the parabola that is given Describe the series of transformations that would move the given parabola to your parabola 2) Write the equation of a parabola that contains the point (0, 8) that is congruent to the parabola that is given




Algebra Ii Module 1 Topic C Lesson 35 Student Version




Graphing Quadratic Functions Lesson Article Khan Academy
State the equation of a parabola congruent to y = 3x2 that has been translated 8 units left and 5 units down from y = 3x2 State the equation of a parabola congruent to y = 2x2 that has been translated 10 units right and 2 units up from y = 2x2 A parabola is congruent to y = x2 Its vertex is (3, 5) State its equation State the vertex andWhat is the y intercept in y=(x2)^22 of a parabola is a vertical line that divides the parabola into two congruent halves Upgrade to remove ads Only $399/month Subjects Arts and Humanities Languages Math Science Social ScienceThe focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus Find the directrix




Ppt Translating And The Quadratic Family Powerpoint Presentation Free Download Id



Vertex Form
A Sketch the graphs on the same axes Label each parabola with its equation b Describe how the value of k in changes the graph of c What happens to the xcoordinates of all points on Congruent to ?The Vertex of the Parabola In this case, we need to find the equation of the graph which is congruent to another graph, thus we know that the coefficient of theIf a) it undergoes a horizontal translation of 3 units left and a vertical translation 4 units down and is congruent to y = v=7x²
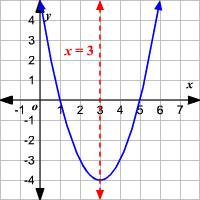



Axis Of Symmetry Of A Parabola



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
Write the new equation of the parabola y = = x?Y (x 21) 2 y (x 2)2 1 The inequality is The inequality is y<(x 1) 2 y »3 x This r will be the radius of the inscribed circle See the following figure, which only shows the top and bottom parabolas, but adds the lines To this end, we compute the derivative
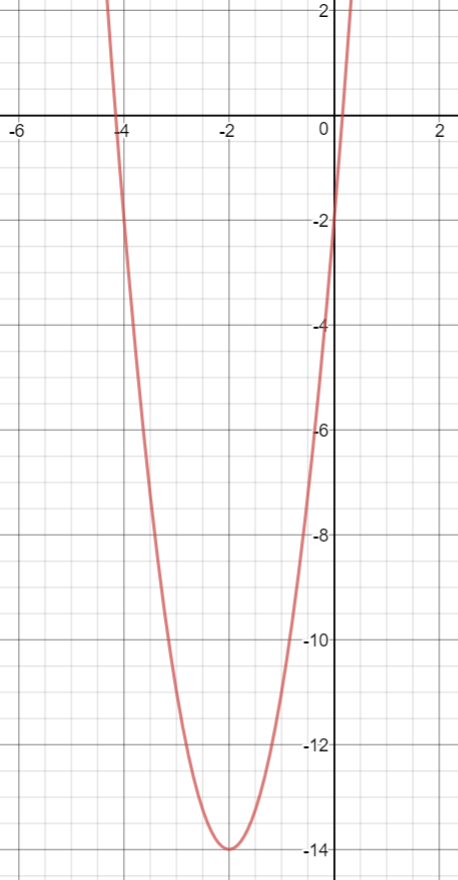



What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic
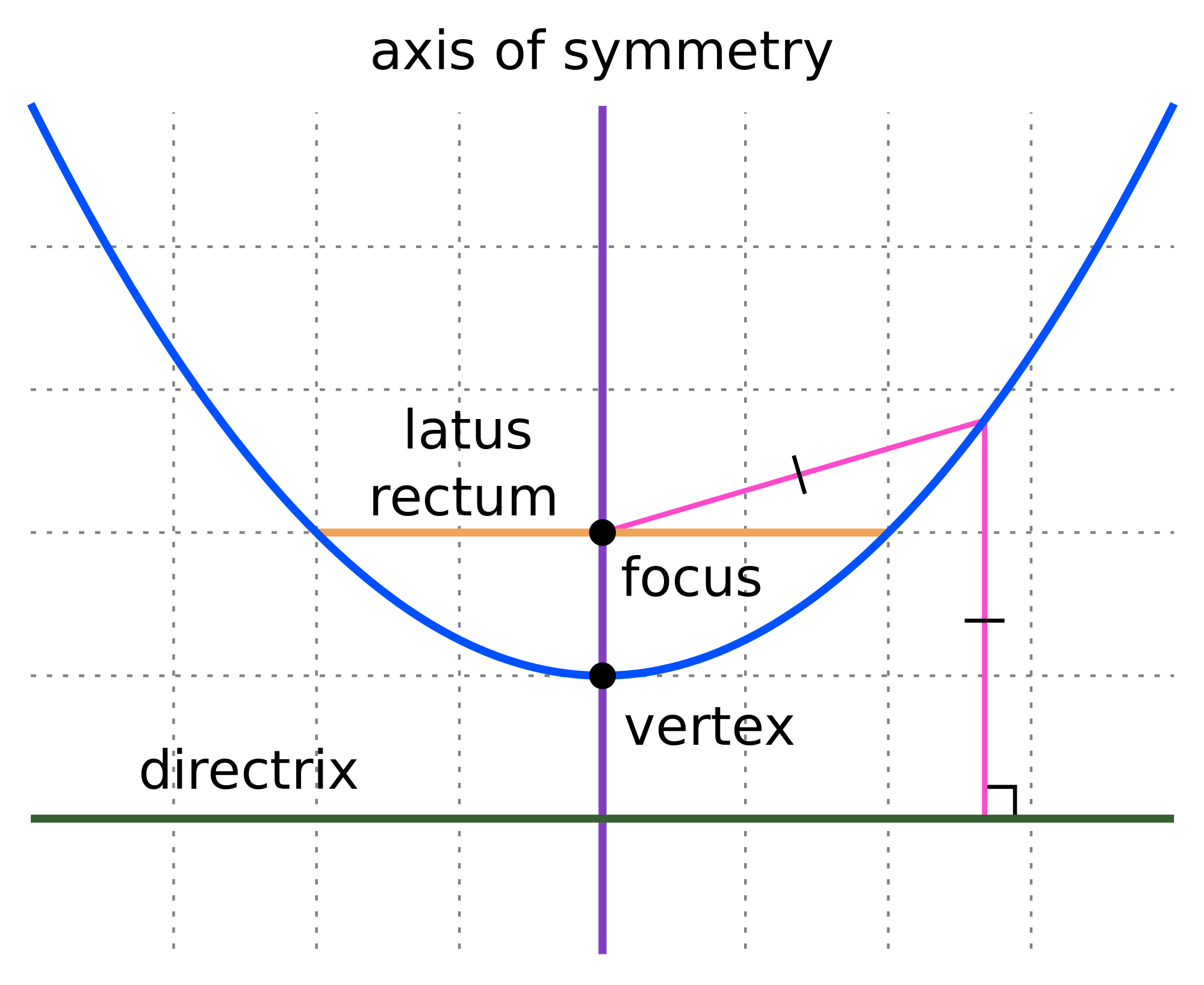



Parabola Wikipedia
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &Parabola described by y = 2x2 is narrower than the parabola described by y = x2 Smaller the coefficient of x2 wider the curveF Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to a parabola with focus (2, 3) and directrix y = – 1?
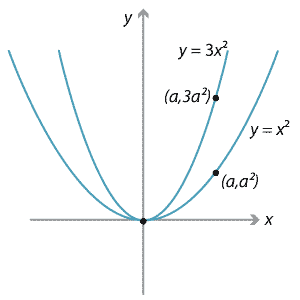



Content Transformations Of The Parabola
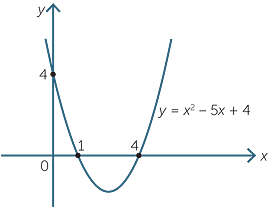



Quadratic Function
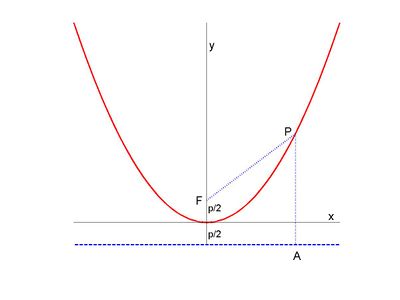
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axisIt is given that the vertex of parabola is at origin (0, 0) and it is symmetric about yaxis So, it's equation is x²= 4ay Or x²The first parabola is translated horizontally to the right by two units and the second parabola is translated down by 3 units, so they each are congruent to the original parabola Exercise 2 Sketch the graph of y = x 2 and the two parabolas you created on the same coordinate axes Answer Exercise 3 Write the equation of two parabolas that




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download



Unique Quadratic Equation In The Form Y Ax 2 Bx C
Explain Answer g Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to the parabola with equation given by y = x 2?We defined the vertex and the axis of symmetry of this graph and we're going to I mean the whole point of doing this problem is so that you understand what the vertex and axis of symmetry is and just as a bit of a refresher if a parabola looks like this the vertex is the lowest point here it's this minimum point here for an upwardopening parabola if the parabola opens downward like thisArc of the parabola y = x 2 I was studying line integral for some pdfs and came up with the following question ∫ γ ( x − 2 y 2) d y, γ is the arc of the parabola y = x 2 from ( − 2, 4) to ( 1, 1) I used the parameterization γ ( t) = ( t, t 2) , γ ′ ( t) = ( 1, 2 t) e ‖ γ ′ ( t) ‖ = 1 4 t 2, but when i do ∫ − 2 1



Parabola Lesson Plans Worksheets Lesson Planet



Graphing Quadratic Functions
Y=x 2 Bu Left Left 4 w = 4 2 so y=(x3) 2_4 a so 1 Y = (x3) ²10 CHAPTER 16 PARTIAL DERIVATIVES Figure 1617 often more useful to sketch a few of its level curves than to sketch that surface Each level curve is the projection of aA parabola is the locus of points which are equidistant from a fixed point, the focus, and a fixed line, the directrix To find the equation of such a curve construct a coordinate system on the plane so that the focus is the point (0,p) and the directrix is the horizontal line y = p A point (x,y) is thus on the curve if and only if the
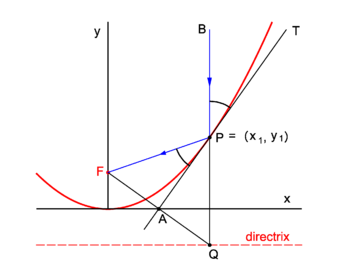



Parabola Knowino
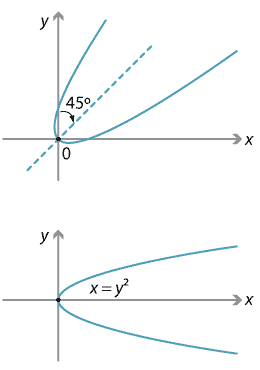



Content Transformations Of The Parabola
Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yWhile a parabola is always symmetric about the vertical line through the vertex (the parabola's axis), the Tchart points might not be symmetric In particular, the Tchart points will not match if the x coordinate of the vertex is something other than aConsider a parabola P that is congruent to y=x^2, opens upward,and has its vertex at (2,4) Now find the equation of a new parabola that results if P is A stretched vertically by a factor of 5 B compressed by a factor of 2




Solved 1 4 Write The Equation For Each Parabola With The Chegg Com
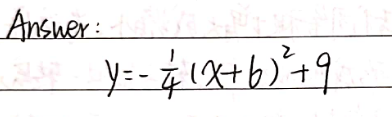



1 A Parabola Has A Vertex At 6 9 Is Congruen Gauthmath
The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves The axis of symmetry always passes through the vertex of the parabola The x coordinate of the vertex is the equation of the axis of symmetry of the parabola For a quadratic function in standard form, y = a x 2 b x c , the axis ofGraph y=x^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola2x =4a dy/dx = 4am where m is slope of the tangent or x=2am Using this value in x^2 =4a^2m^2 = 4ay gives y = am^2 That means the tangent touches the parabola at (2am,am^2) Now equation of tangent is y=mxc and it passes the above point so am^2 = 2am^2c or c= am^2



2




Content Transformations Of The Parabola
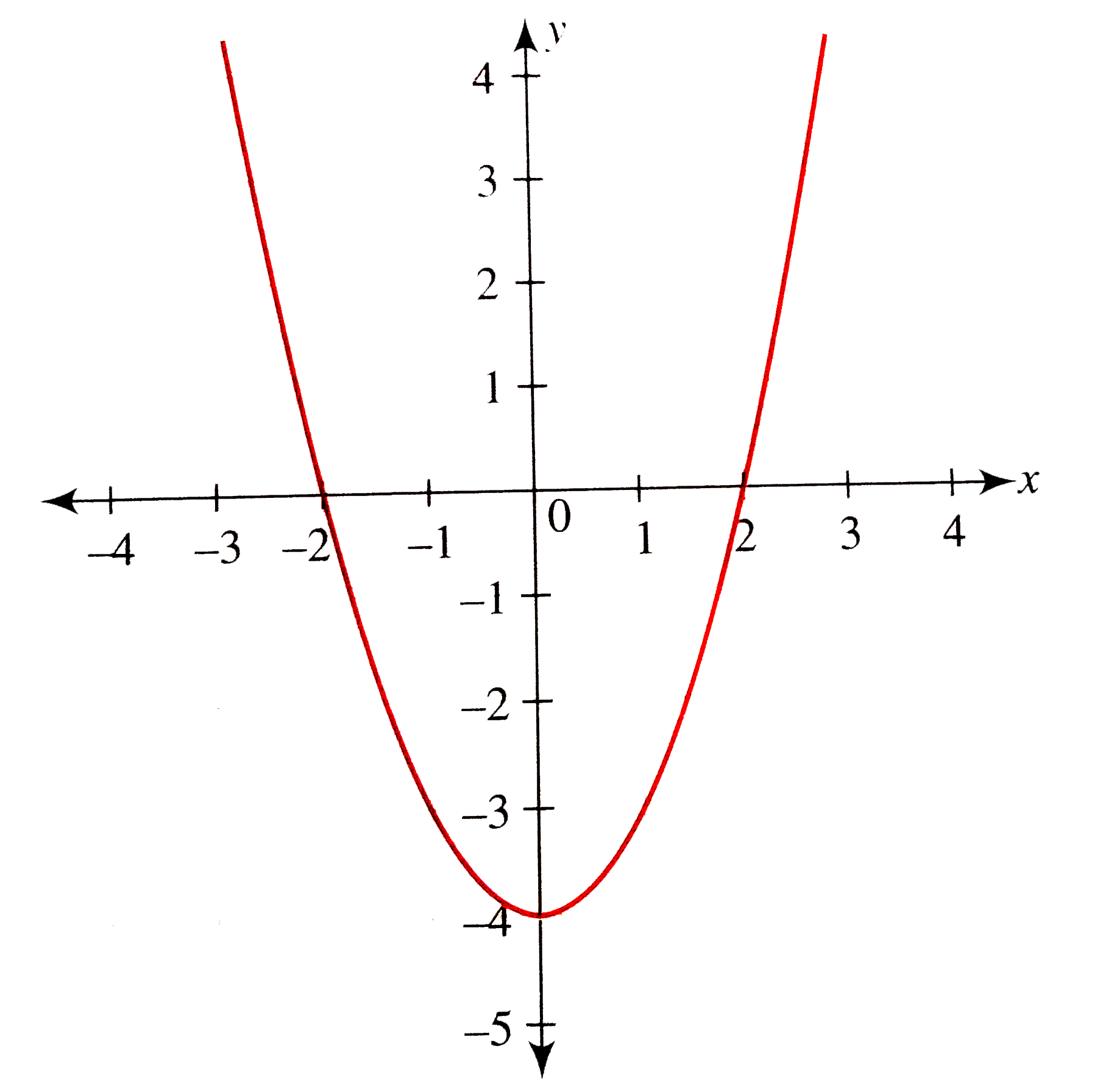
In each case complete the square and determine the xand y ‑intercepts, the axis of symmetr y and the vertex of the parabola a y = – x 2 8 x 13 b y = – x 2 – 3 x – 5 c y = – x 2 – 10 x THE STRETCHING TRANSFORMATION The transformations dealt with so far have produced parabolas that are congruent to the basic parabola y = x 2A parabola is congruent to y=x^2 and has xintercepts 1 and 5 determine the coordinates of the vertex Answer by Fombitz () (Show Source) You can put this solution on YOUR website!
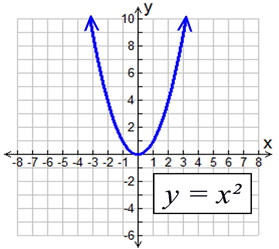



Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Axis Of Symmetry Of A Parabola




How To Find The Vertex Of A Quadratic Equation 10 Steps
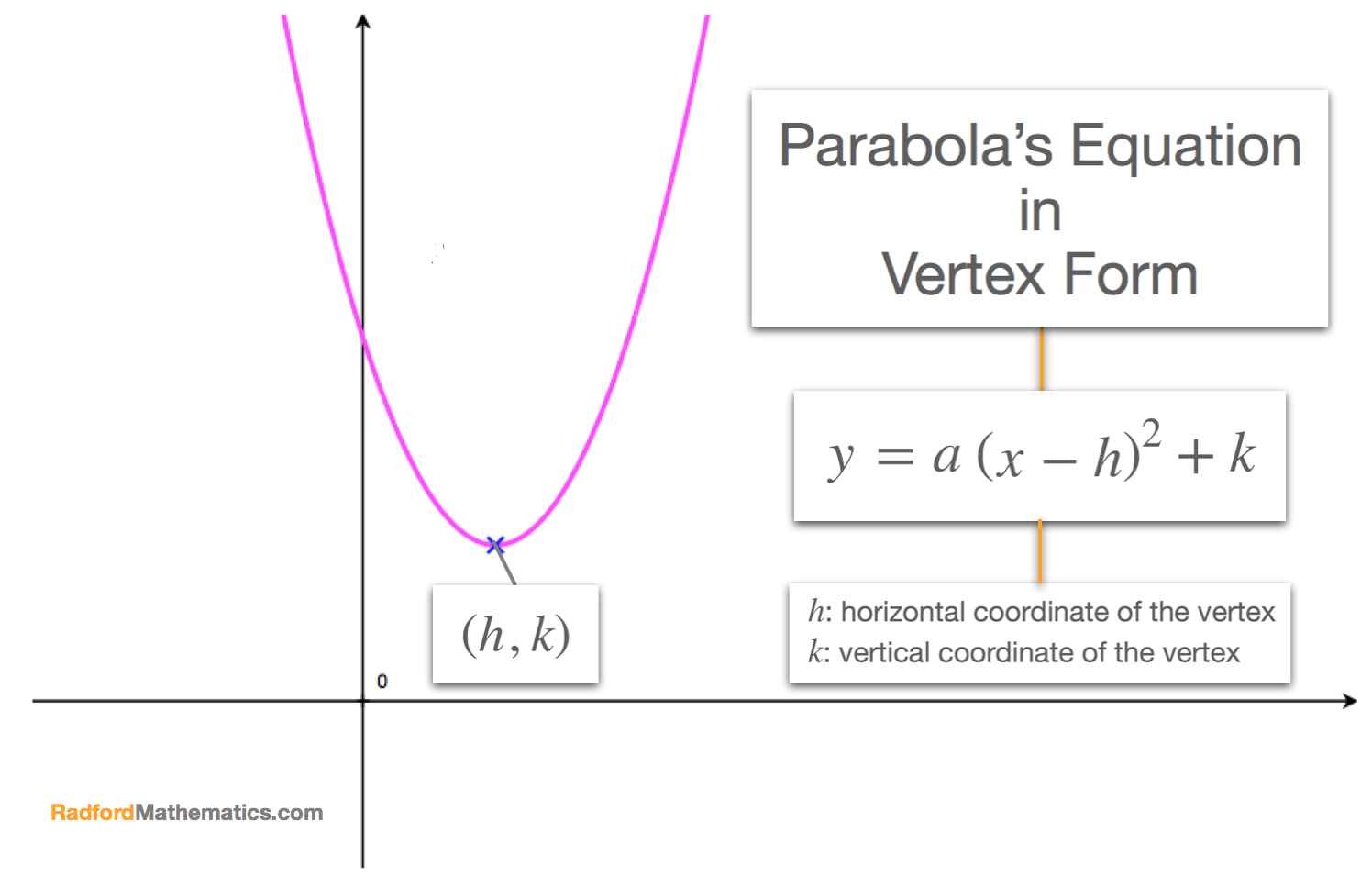



Vertex Form How To Find The Equation Of A Parabola




Plot A Graph For The Equation Y X 2 4x 1




Parabola Wikipedia




Quadratic Equation Congruent To Parabola Pass Through Point With Y Intercept As Another Curve Youtube



Identifying Roots And Turning Points Of Quadratic Functions Gcse Mathematics Edexcel Revision Study Rocket



Graphing Quadratic Functions




Answered The Focus Of A Parabola Is 3 5 And Bartleby



Math Spoken Here Classes Quadratic Equations 3



Unique Quadratic Equation In The Form Y Ax 2 Bx C



What Is The Area Enclosed Between The Parabola Y X 2 And The Straight Line Y X Quora



Congruent Parabolas Youtube




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation



Graphs Of Quadratic Functions Boundless Algebra




Vertical Shifts Of Quadratic Functions Ck 12 Foundation




Scaling Reflecting Parabolas Video Khan Academy



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph



Blessedmotherteresa Typepad Com Files Graphingquadratics Day3 Pdf



Math Spoken Here Classes Quadratic Equations 3




7uyexnxeeznwvm



1



Axis Of Symmetry Of A Parabola




Parabola Parent Function Mathbitsnotebook A1 Ccss Math




2 Marks 4 If The Point 2 7 Is On The Parabola Y Chegg Com




Resourceaholic Tricks And Tips 3 Quadratics




Solved 5 Consider A Parabola P That Is Congruent To Y X Chegg Com




Graphing Quadratic Functions Lesson Article Khan Academy




How To Find The Vertex Of A Quadratic Equation 10 Steps




Quadratic Function
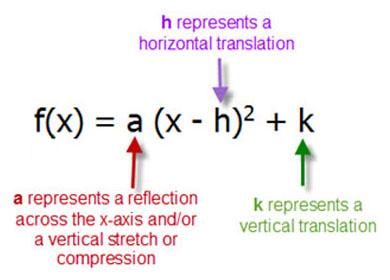



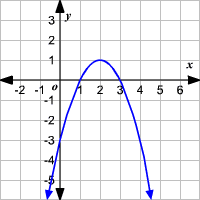
Untitled Document
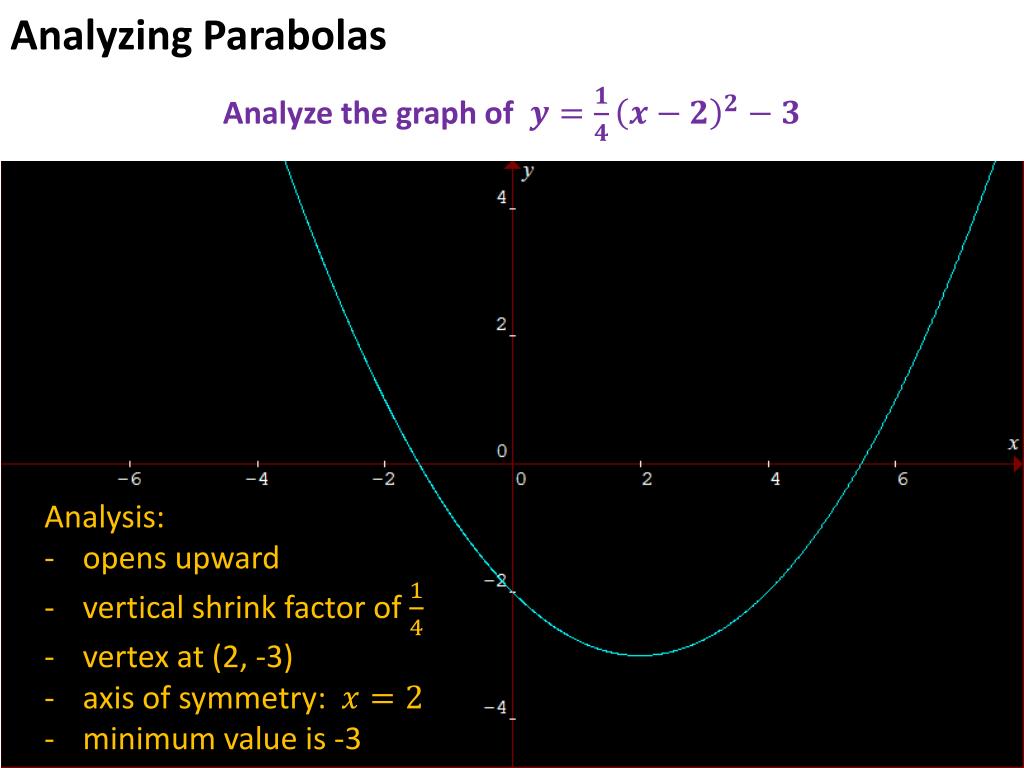



Ppt Analyzing Parabolas Powerpoint Presentation Free Download Id




Attributes Of Quadratic Flashcards Quizlet




How To Calculate The Y Intercept Of A Parabola Quora



1
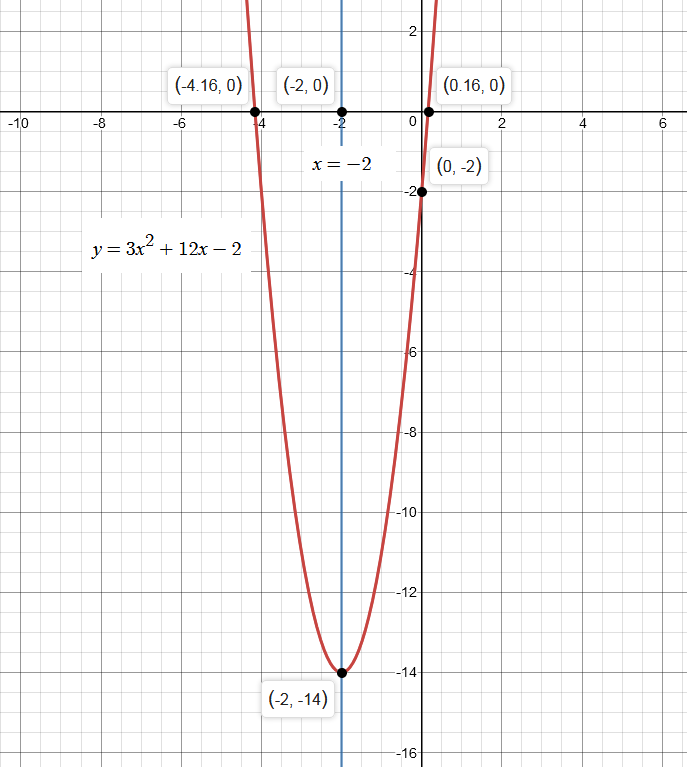



What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic



Solution Find The Equation Of The Parabola With Vertex 4 4 The Parabola Opens Upwards And Is Congruent To Y 1 2x 2 Can You Please Help Me Thanks So Much In Advance



Math Spoken Here Classes Quadratic Equations 3




Resourceaholic Tricks And Tips 3 Quadratics




Content Transformations Of The Parabola



1



How To Calculate The Y Intercept Of A Parabola Quora



L2d2ii Html




Sketch A Graph Of The Parabola Y X 2 3 On The Same Graph Plot The Point 0 6 Note There Are Two Tangent Lines Of Y X 2 3



What Is The Equation Of The New Parabola Created By Shifting Y X2 Three Units In The Positive Y Axis Direction Quora




Parabola Wikipedia
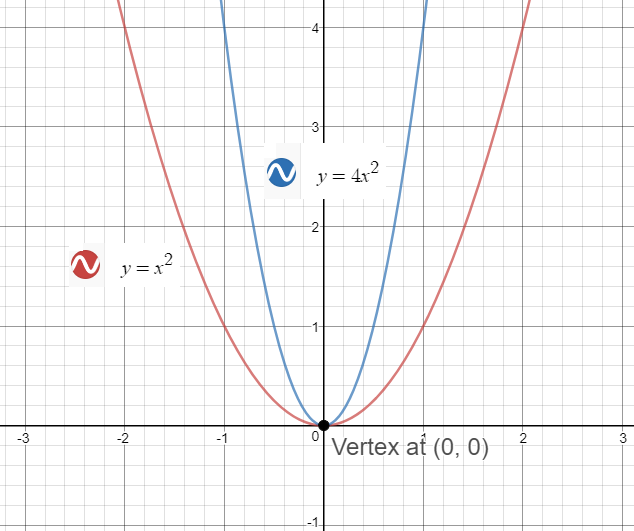



How To Graph A Parabola Y 4x 2 Socratic
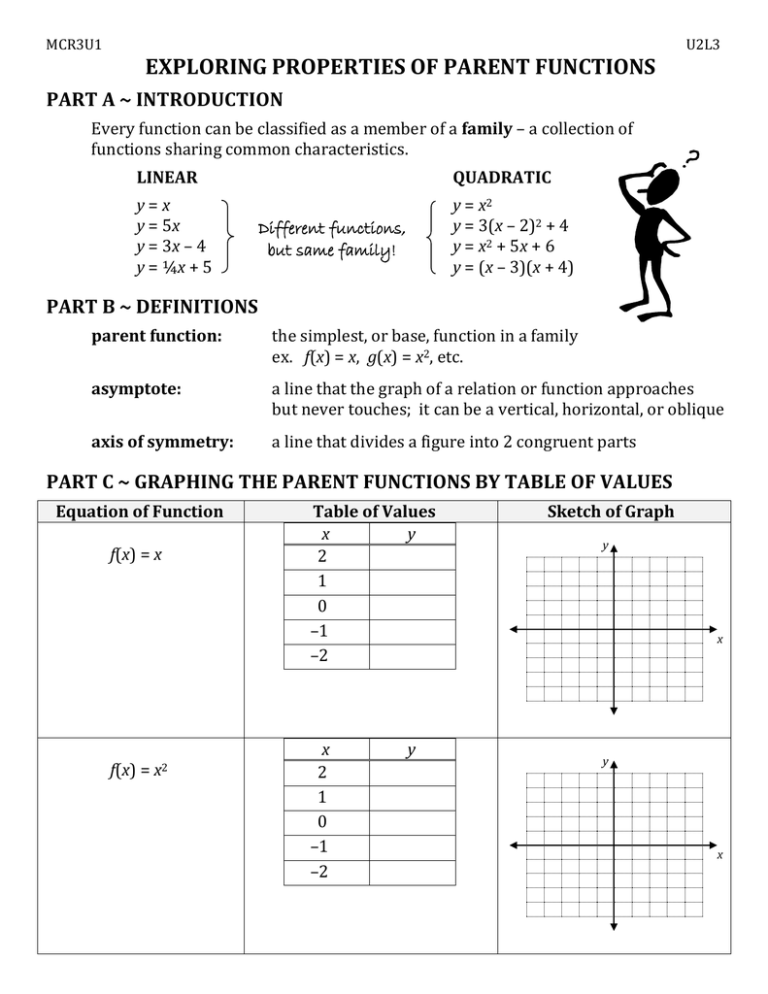



Exploring Properties Of Parent Functions Part A Introduction




How To Find The Vertex Of A Quadratic Equation 10 Steps




Shifting Parabolas Video Khan Academy



Exploration Of Parabolas




Draw The Graphs Of Following Quadratic Functions I Y X 2




Quadratic Functions Academic Support Center
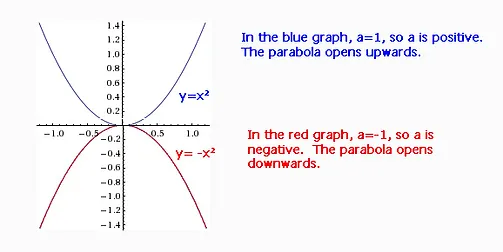



Vertex Form Chapter 4 Quad Relationships
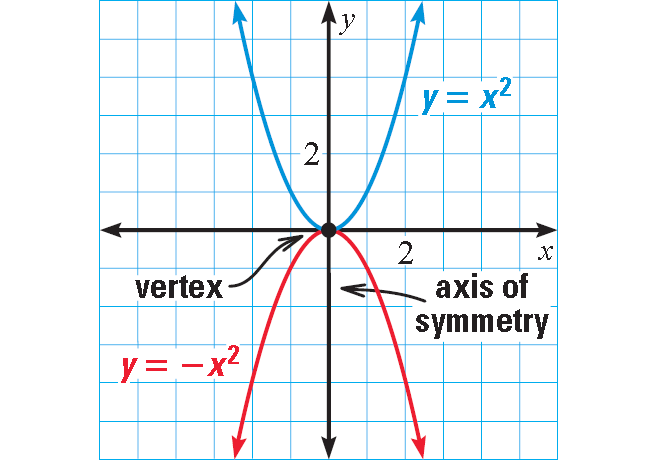



Graphing Quadratic Functions Parabola



The Parabola




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



Graphing Quadratic Functions
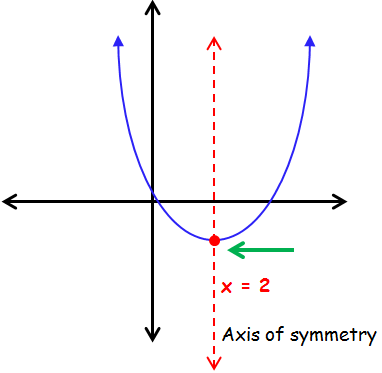



Characteristics Of Quadratic Functions
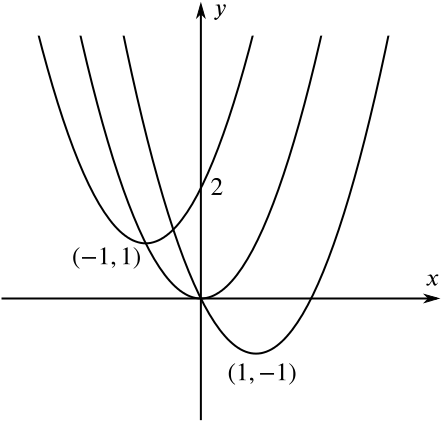



Solution Into How Many Regions Do These Parabolas Divide The Plane Quadratics Underground Mathematics




The Axis Of The Parabola Y 2 2x 0 Is
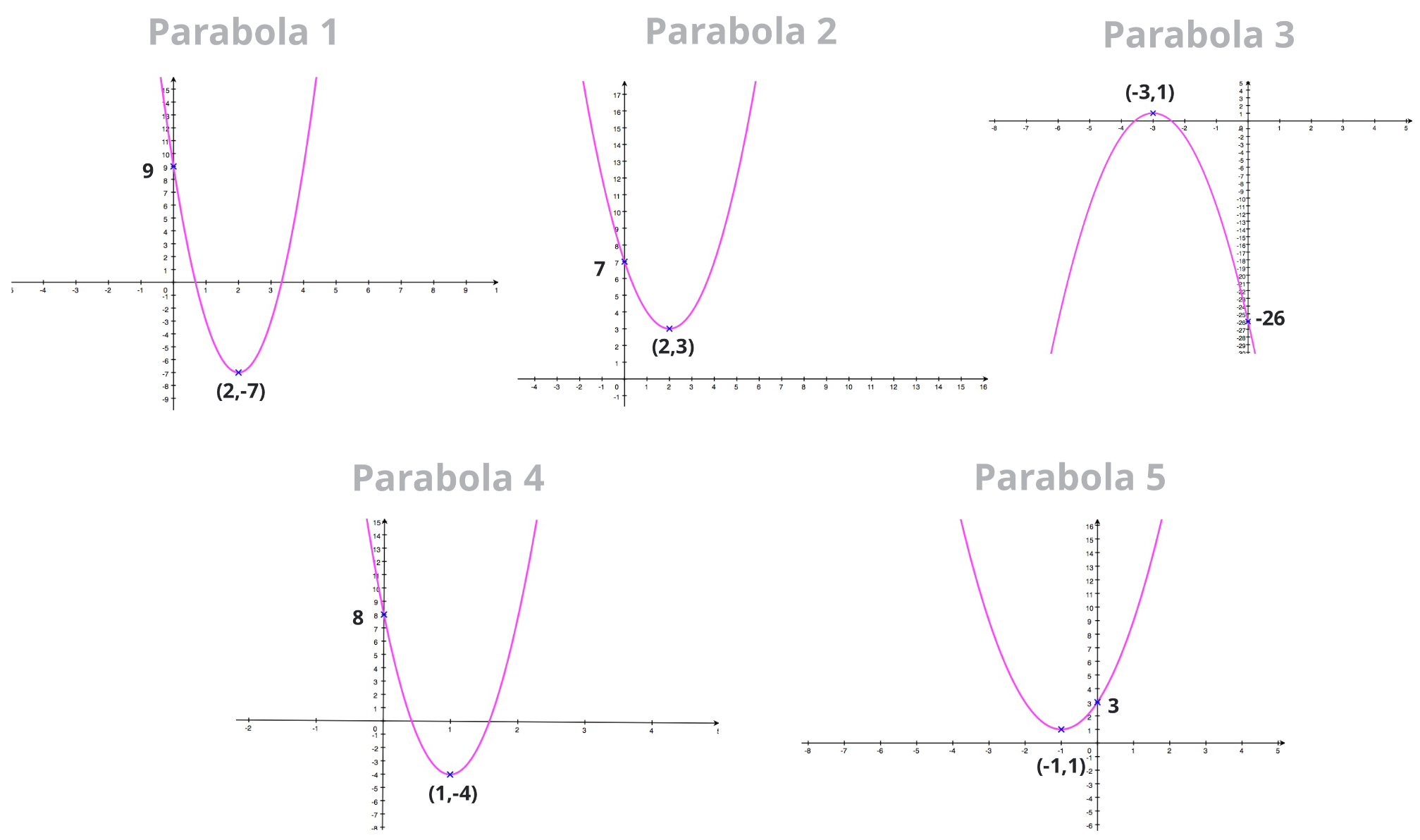



Vertex Form How To Find The Equation Of A Parabola
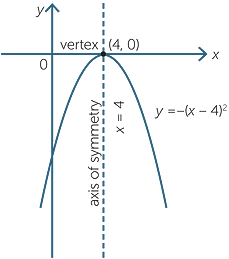



Quadratic Function




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download
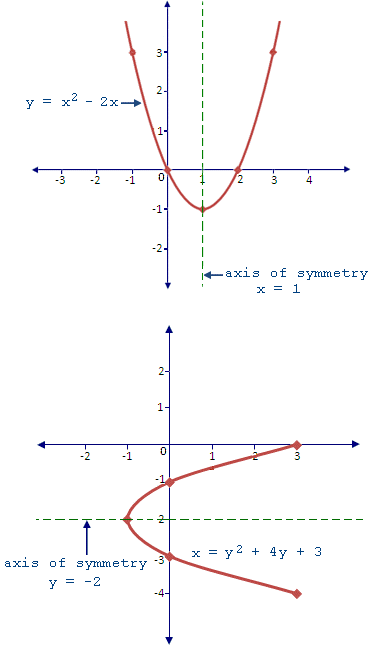



Axis Of Symmetry Of A Parabola



Www Engageny Org File Download Algebra Ii M1 Topic C Lesson 34 Teacher Pdf Token D04trqow




0r199j Fuiupsm
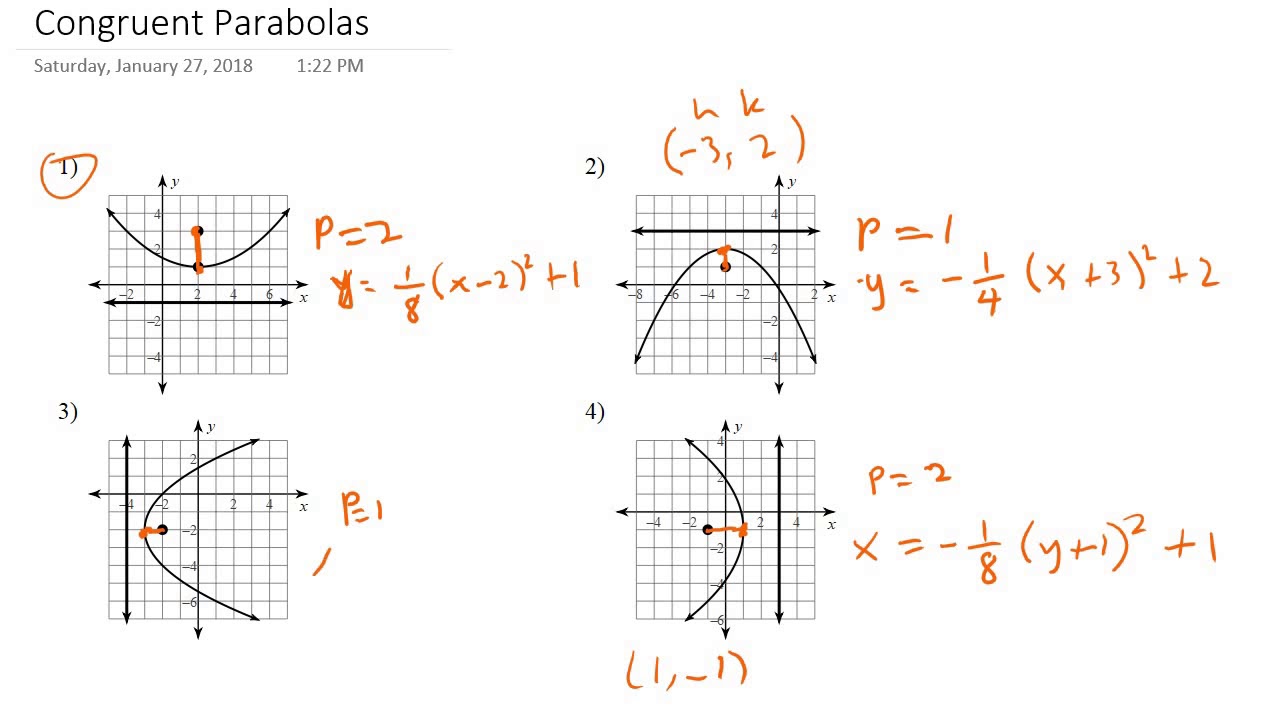



Congruent Parabolas Youtube



What Is The Equation Of The New Parabola Created By Shifting Y X2 Three Units In The Positive Y Axis Direction Quora




Quadratic Function




Quadratic Functions Academic Support Center
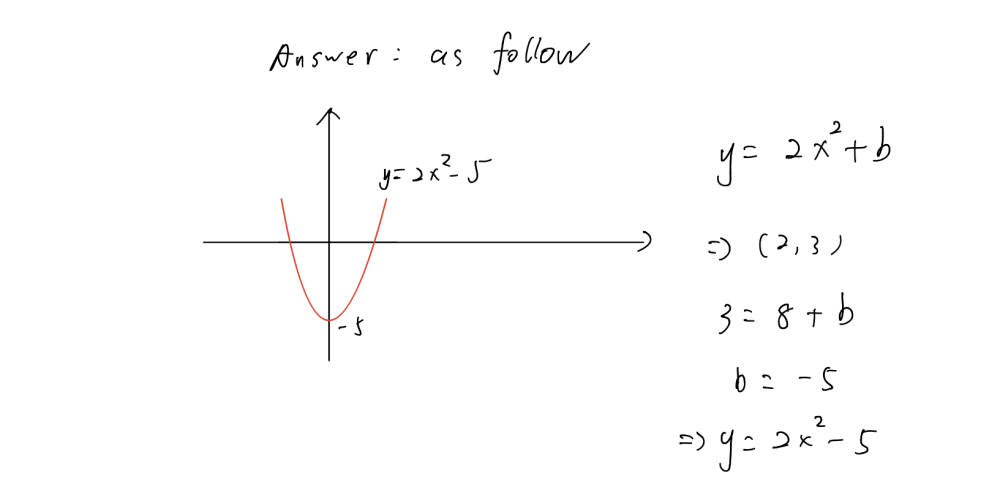



Vrite The Equation Of A Parabola That Matches The Gauthmath



0r199j Fuiupsm



0 件のコメント:
コメントを投稿