1 単元名「垂直平行と四角形」 までの学習では,図形をとらえる視点として,「辺や頂点の数」「辺の長さ」「角の大きさ」に着目し てきた。本単元では,「平行」「垂直」「対角線の交わり方や長さ」という新たな視点が加わることと なる。 4 こんな内容を 本単元では,図形についての三角形の面積の公式、底辺、高さを確認する。 本時で面積を求める三角形と前時の三角形の違いを確認する。 学習課題を確認する。 「頂点が底辺の延長線上にある三角形の面積も、「底辺×高さ÷2」で 求められるか確かめよう」 ・電子黒板頂点が黒い四角で表示されて頂点の編集モードになります。 ② 図形の頂点を右クリックし、頂点を中心にスムージングするをクリックします。 ③ 頂点でカーブした形になり、黒い頂点から白い四角のハンドルがついた棒が表示されます。この白い四角
四角形で向かい合う頂点を直線を結ぶ その直線を対角線という Yahoo 知恵袋
四角形の頂点 英語
四角形の頂点 英語-垂直・平行と四角形2 子どもの学習支援 by いっちに算数 スマホ版 前のページにもどる 教え方3 教え方3① 上の四角形を平行な辺の組の数で仲間わけをして、台形と平行四辺形を教えます。 12組の辺が平行な四角形 21組の辺が平行な四角形三角形の頂点の色を変更してみて下さい。 四角形を表示してみて下さい。 四角形は三角形を二個組み合わせて表示します。 三角形のポリゴンを組み合わせて四面体を表示してみて下さい。 独立した三角形を組み合わせることもできますが、隣り合った三角形の一辺がつながるように頂点を



四角形の分割
四角形に条 じょう 件 けん エ2本の対角線が交わる点から4つの頂点 までの 長さがすべて等しい。 正方形は,とても条件の多い四角形なんだね。 正方形についてわかったことを書きましょう。 2 3 長方形 平行四辺形 正方形 四角形 ひし形 3 5 4 1 2 ・2学年での四角形,3学年での正方形と長方形DirectX11プログラミング 四角形・五角形・六角形サンプルの三角形を四角形にしてみます 要するに,ポリゴンを増やすにはどうするのか? と言う話です(だと思う) 頂点数が3つで三角形,4つで四角形だと,単純に考えて(''*)頂点 の数 2つの 底面 が平行 で, 形と大きさが 同じ多角形 に なっている 立体 を, 角柱 といいます 。 2つの 底面 が平行 で, 同じ大きさの 円になってい る立体 を, 円柱といいます 。 角柱 で,底面 の形が三角形 ,四角形 ,五角形 ,の立体 を,
四角形 、角丸四角形 一度でも「頂点 の編集」を行うと、図形は単なる多角形という扱いになり、特殊ハンドルは表示されなくなります(3–16 多角形と図形の編集参照)。なお、今図形がどのような扱いになっているかはオブジェクト一覧で確認できます(3–26 オブジェクト一覧参照 図形と方程式|平行四辺形の頂点の座標について 数学2 今回は、平行四辺形の頂点の座標について学習しましょう。 ここでは、平行四辺形を作るとき、4つの頂点のうち3つが既知で、残りの頂点の座標を考えます。 図形を扱った問題では、三角形や四角形が題材としてよく用いられます。 演習をこなして慣れておきましょう。 目次 1 平行四辺形 頂点 1、 n 1、 n 2 は三角形 n を定義します。 N ~ 2 個 の三角形が描画されます。 GL _ 四角形 4つの頂点の各グループを独立した四角形として扱います。 頂点 に**は、 四角形 n が定義さ れて**います。 N/4 quadrilaterals が描画されます。 GL _ QUAD _ ストリップ
図形の四角形の右下の黒い頂点を左上に向かってドラックしてみましょう。 形が四角形から変わりました。 黒い と白い をドラックするといろいろ変形できるので試してみてください。 白四角をドラッグすると線がカーブします。 頂点を右クリックすると、スムーシングなどができます。四角形の中にできる平行四辺形その5中点連結定理の応用です。 12.四角形の重心四角形の重心はどのようにして求めるのでしょうか。 11.三角形の問題三角形ABCの各辺の三等分点を順に結ぶと、それぞれの辺はどのような関係になるでしょうか。 10.下の図で四角形 は相似の関係にあるといえる。 相似な図形は形が同じなので対応する頂点、辺、角がある。 対応する頂点は・・・↓画像を5回クリック! 対応する辺は・・・↓画像を5回クリック! 対応する角は・・・↓画像を5回クリック! 特に辺の場合は頂点に対応してかくよ うに
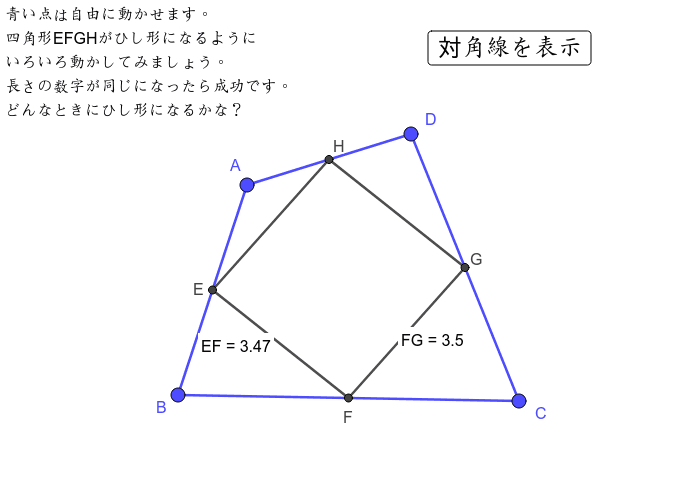



四角形abcdの各辺の中点を結んでひし形を作ろう Geogebra
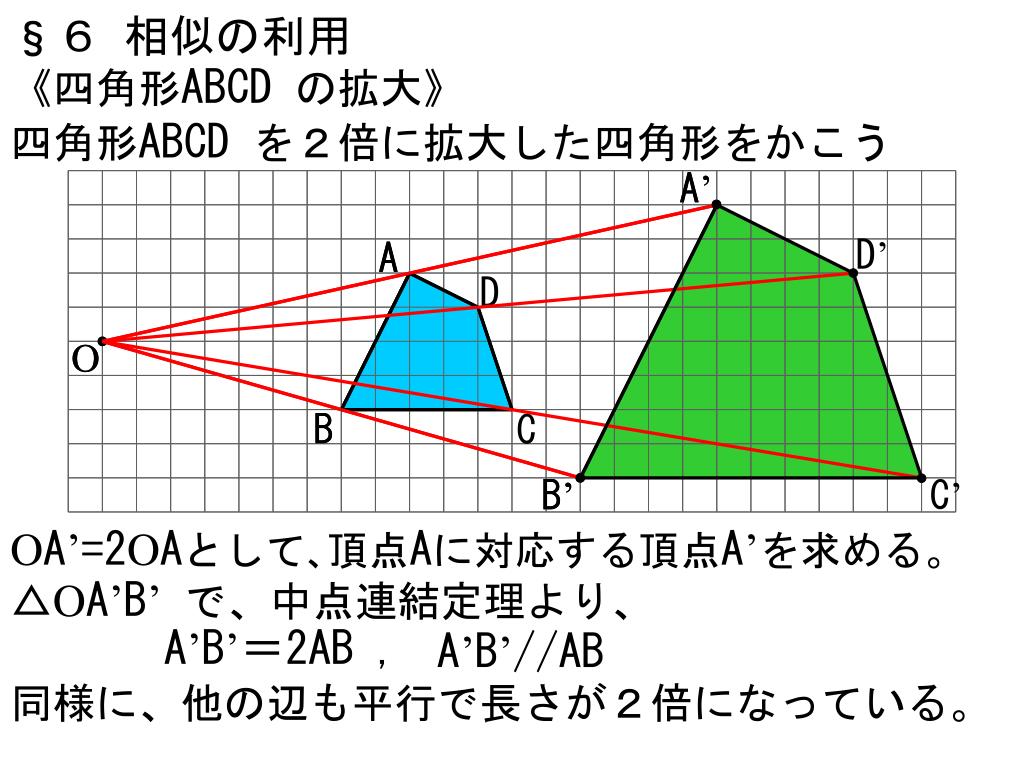



Ppt 5 図形と相似 Powerpoint Presentation Free Download Id
・四角形の描写: 頂点をスナップ、ドラッグ、又は座標値の入力。図心ドラッグ可。 (他:一体移動、回転、領域の設定、三角形の描写) 図心ドラッグ可。 「四角形の定義」 4本の線分で囲まれた形。4つの頂点と辺を持つ形。 注:「四角形の 定義 」で「平面上で4本の直線に囲まれた形」とされることもあるが、 「4本の直線」だと「凹四角形」が切れてしまうので、「4本の線分」とする。図形の形を変更する ホーム タブのツール グループで、四角形 タブの横にある クリックし、鉛筆ツールタブをクリック 。 図形を選択し、移動 頂点をクリックして、頂点を新しい位置にドラッグします。 ページの先頭へ



晃華学園11 2 組み合わせ 八角形の頂点を結んで三角形や四角形を作る 気まぐれ解説カフェ 仮



Www Pref Mie Lg Jp Common Content Pdf
3 多角形の面積の求め方 6 p;q;r;s のみが与えられている場合では四角形の形状は決定できない きちんと周回順に与えられたとして も, それだけでは形状は一意に定まらない 四角形の頂点座標が座標平面上で与えられている場合が最も多いだろう 次は、vertex(頂点)を使用した図形の描画描画です。 これを使うと、様々な形の図形を描くことができます。 まずは、beginShape ()で形を描くことを宣言し、vertex (x, y)で一つずつ頂点を指定していきます。 次に、四角形を描いてみます。 ここでのポイント 三角形(頂点を A, B, C とし、その対辺の長さをそれぞれ a, b, c とする)の面積を求める方法には、次のものが知られている。 (底辺)×(高さ)÷2 (1/2)ab sin∠C ヘロンの公式 (Heron's formula) √(s(sa)(sb)(sc)), ただし, s=(abc)/2;
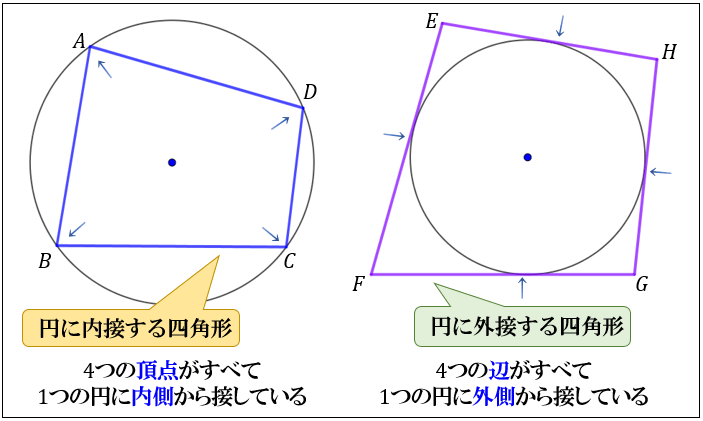



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



四角形で向かい合う頂点を直線を結ぶ その直線を対角線という Yahoo 知恵袋
2年「三角形と四角形」 氏名 三角形や 四角形で まわりの ひとつひとつの直線を 辺 へん かどの点を ちょう点 てん といいます。 3本の直線でかこまれている形を 三角形 さんかくけい といいます。 4本の直線でかこまれている形を 四 し 角形 かくけい といいます。進研ゼミからの回答 特に書く順序は気にする必要はありません。 ただし,合同な図形において角や三角形を表すときは,対応する頂点の順序に書く必要があります。 ここで紹介している内容は17年3月時点の情報です。 ご紹介している内容・名称等は変わることがあります。 ※ このQ&Aでは、 「進研ゼミ中学講座」 会員から寄せられた質問とその回答の一部を 長方形の描画が正方形になると、四角形の内側に対角線ガイドが表示されます。 楕円の描画中に真円になる位置にくると、円の内側に十字線ガイドが表示されます。 隣接するオブジェクトを正確に整列させる スマートガイドを表示すれば(表示/スマートガイド)、アートボード上でオブ




すきるまドリル 小学2年生 算数 三角形と四角形 無料学習プリント すきるまドリル 無料学習プリント




3d または 2d 図形の投影を使用した 2d 図形の作成
頂点を選択すると、白四角のハンドルが表示されます。 白四角をドラッグすると線がカーブします。 下図のようにちょっと曲がった矢印ができました。 頂点を増やすこともできます。 頂点の編集状態にして、線をドラッグして変形すると、頂点が追加されます。 または、線上で右クリックし三角形の四角形への結合の手順 エディットモードで結合する隣り合う三角形の面を選択し、キーボードのALT Jを押します。 頂点選択モードでの三角形の四角形への結合 上図のように頂点選択モードでは、選択中の隣り合う三角形の面が四角形に結合され・四つの一般四角形のそれぞれの角に着色し、一つの頂点に四つの角が集まり、四角形の内角の和でもある 360°を作っていることを見付けやすくする。 平行四辺形の一部を変形させ、四角形を敷き詰めて、幾何学模様を作る。 ・平行四辺形のどこをどのように変形したのかに注目してお互いの
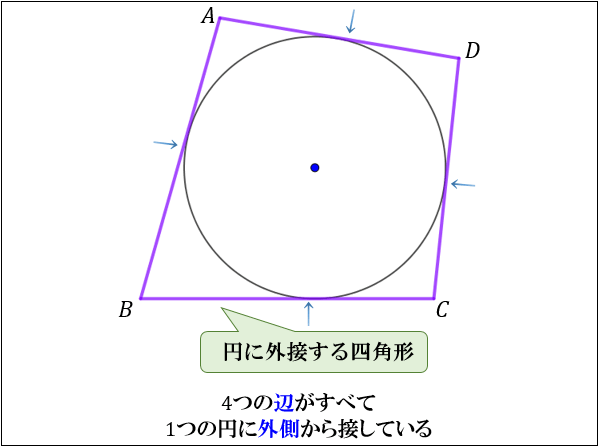



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ




思い通りの図形を作成するための頂点の編集テクニック ノンプログラミングwebアプリ作成ツール Forguncy フォーガンシー グレープシティ株式会社
四辺形と四角形は同じ形なので、四角形をquadrilateralとも言います。 A quadrilateral has ・four sides (edges) ・four vertices (corners) ・interior angles that add to 360 degrees (筆者訳)四角形は ・4つの辺、 ・4つの頂点、 ・内角の和が360° である。 出典:*1 An Quadrilateral(四角形 四角形(しかくけい、しかっけい、英 quadrilateral, tetragon )は、 平面上で4本の直線に囲まれた平面の一部を指す。多角形の一種で、 4つの頂点と4本の辺を持つ。 引用先:Wikipedia 定義上は四角形である しかし四角形の種類の中に台形・長方形・平行四辺形等の中に 凹四角形というものがあっ四角形の4つの辺の中点を結んでできる四角形 はじめに この問題は,GCにとって,とても重要な問題である



四角形abcdの各辺の中点を結んで長方形を作ろう Geogebra




鯵坂もっちょ در توییتر こちら 足すとフィボナッチ数になるような2数をつないだもの です これをよく見るとどうやら 四角形しかない 四角形の対頂点の差がフィボナッチ 四角の左上がリュカ数 四角の右上がフィボの2倍 などの構造が見えて 昨日の
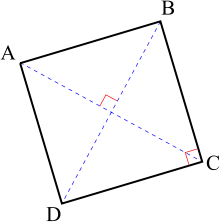
正方形の頂点を最短距離で結ぶ 次は,正方形の4頂点を結ぶ場合を考えます。 愚直な方法:一辺が1の正方形の三辺を選んで結ぶと長さの和は3になります。 少し工夫した方法:真ん中に分岐点を1つ作って X X X 型に結ぶと長さの和は 2 2 ≒ 28 2\sqrt {2凹四角形 内角の大きさが180°(π ラジアン) を超えるような頂点を持つ四角形。対角線が四角形の内部で交点を持たない、外角が定義できないなどの不都合があるため、日本の初等中等教育では「矢じり形」などと呼んで、四角形の集合には含めない。




基本のquadrilaterals 四角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



小学2年生の娘がテストで をもらって来ました 四角形は4つの Yahoo 知恵袋



1



四角形 ひし形 平行四辺形 台形 の書き方 作図 まとめ 受験辞典



入試問題に挑戦第61回




Aop Ps Oc Descubre Como Resolverlo En Qanda
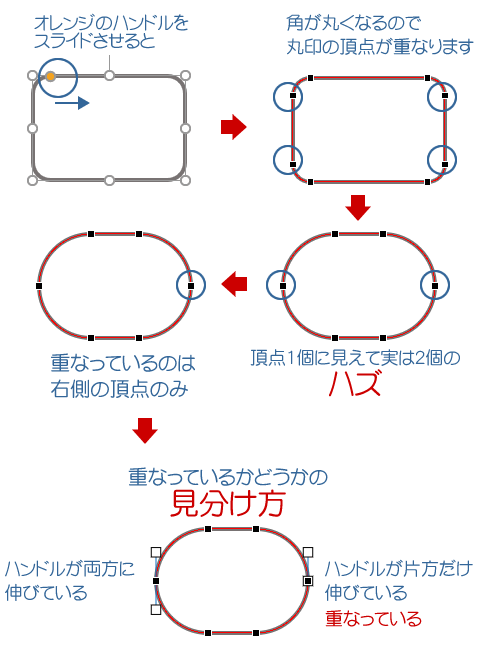



図形の角丸四角形の頂点の癖を理解してお絵かきしよう Wordあそび



辺と算数の関係は 1分でわかる意味 四角形 立方体の辺の数 順番



四角形 ひし形 平行四辺形 台形 の書き方 作図 まとめ 受験辞典




正方形 Wikipedia




Abcd Bad 1 Descubre Como Resolverlo En Qanda



図形の扉 四角形の性質




基本のquadrilaterals 四角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



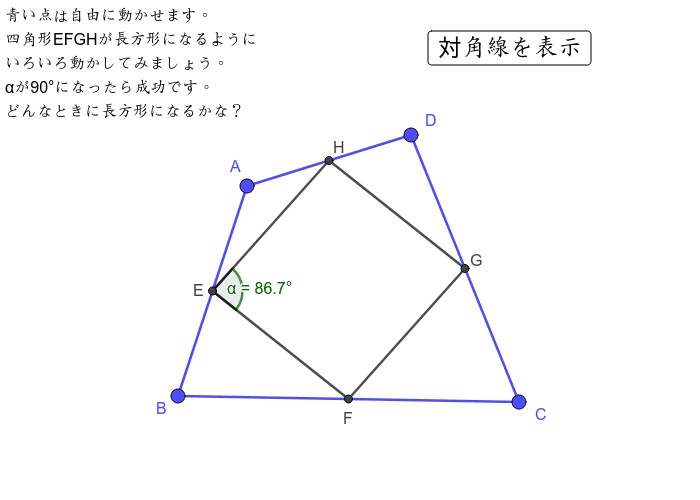
4年算数 垂直 平行と四角形 2 教え方



合同な三角形を記号で表す場合 対応する頂点の名前を周にそって同じ Yahoo 知恵袋




Blender 三角形化 四角形化 扇状化の使い方 Blenderの易しい使い方
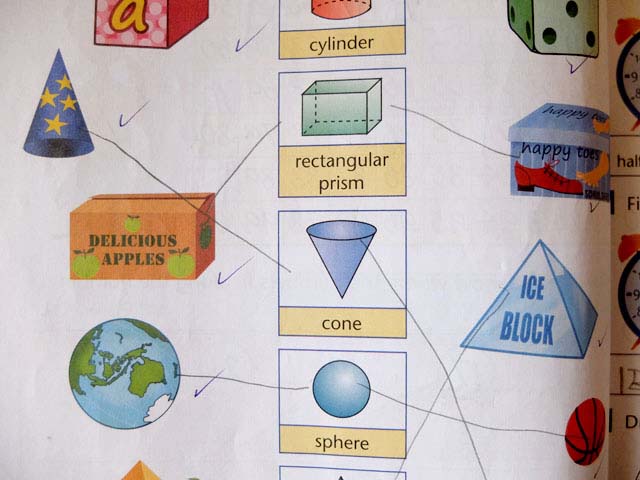



意外と知らない 英語で基本的な図形の名称と表現を覚えよう 話す英語 暮らす英語



四角形に関する様々な関数 その 1 ぐらの倉
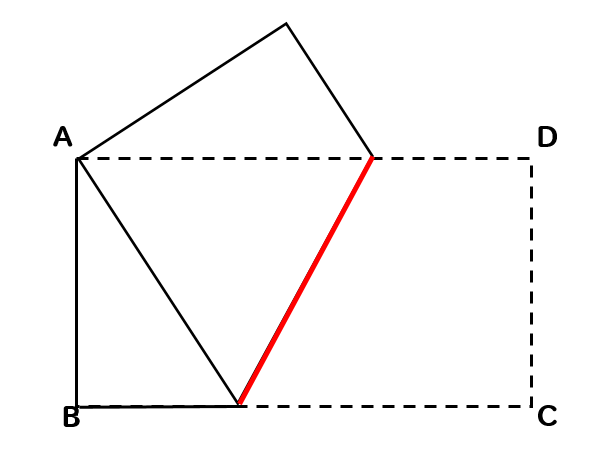



コンパス作図 長方形 正方形の折り目を書く方法を問題解説 数スタ



対角線で参観 教育考現学



図形の角丸四角形の頂点の癖を理解してお絵かきしよう Wordあそび



Projectivegeometry



Qsj1984 Com Wp Content Uploads 05 62b45d2f8c69a8dda2c0b3bb Pdf



体が求める 四角形を Eroshin S Blog




Abcd Ab6cm Abard8cm P Descubre Como Resolverlo En Qanda
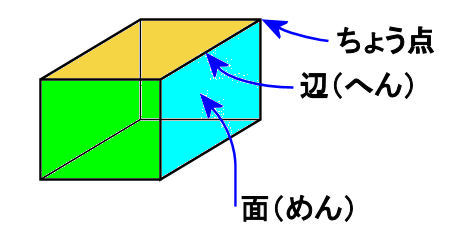



頂点 辺 面




答1044 凸多角形と頂点を共有する四角形 ヤドカリの 気ままな数学



Www Edu City Yokohama Jp Sch Kenkyu Es Sansu Pdf R1 Teian R1924 Pdf




エフェクトオブジェクト解説




立方体と直方体の面 辺 頂点 Youtube
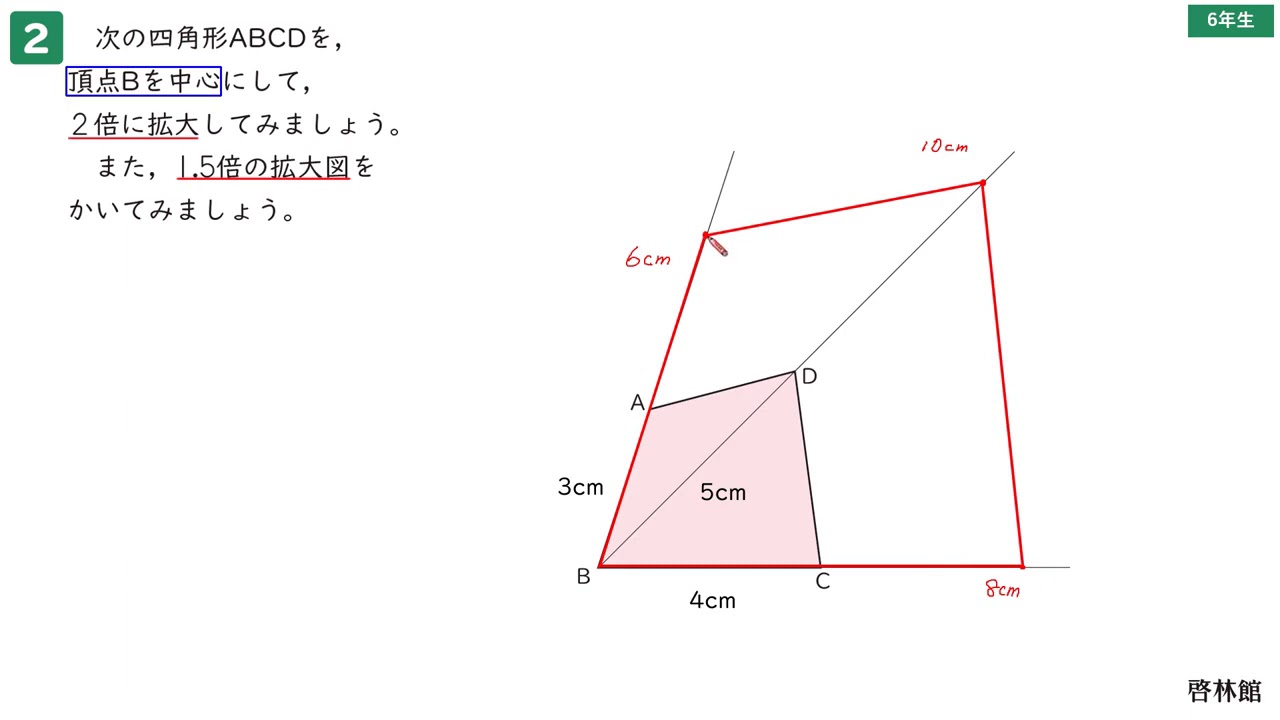



図形の拡大と縮小 拡大図と縮図のかき方 02 1つの点を中心にして Youtube
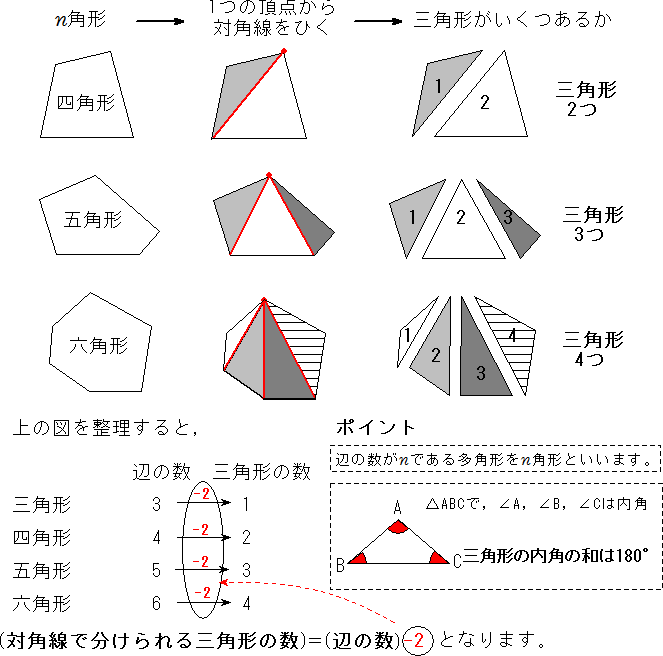



三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト
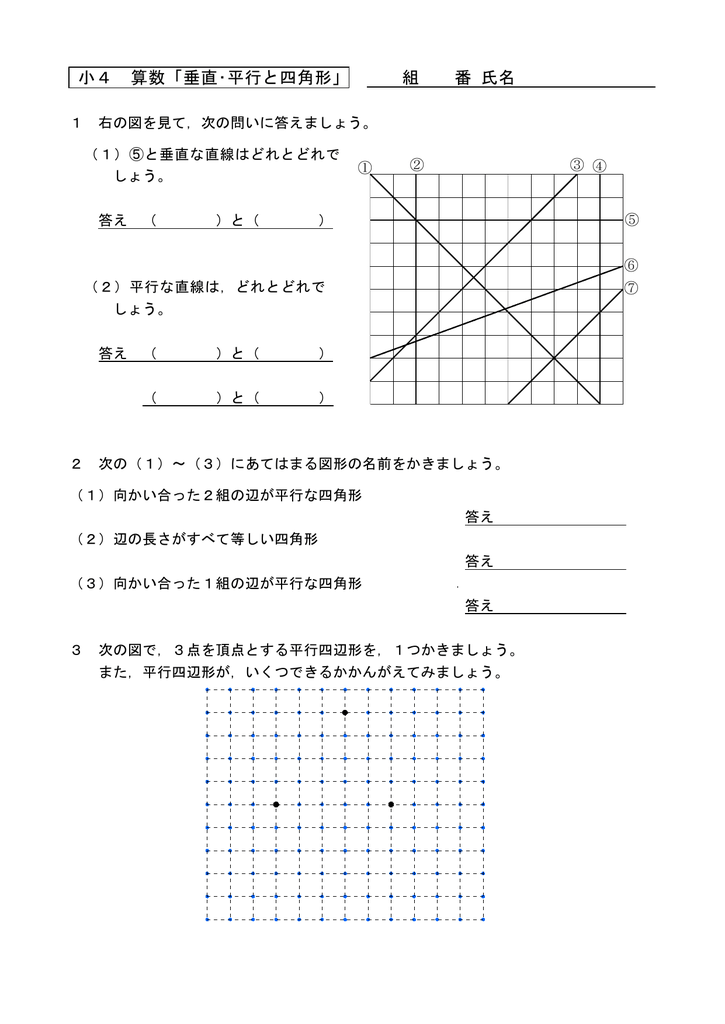



小4 算数 垂直 平行と四角形 組 番 氏名



四角形の分割




凹んだ四角形 小2の宿題で大困惑 コレは四角形 なかしんの鹿児島育児ブログ



図形と組合せ 円に内接する多角形 教えて数学理科



数学 三角 四角 辺と頂点 編 Teach U 特別支援教育のためのプレゼン教材サイト



小学2年生の算数 三角形と四角形 直角三角形 正方形 長方形 辺 頂点 直角 練習問題プリント ちびむすドリル 小学生




ページタイトル
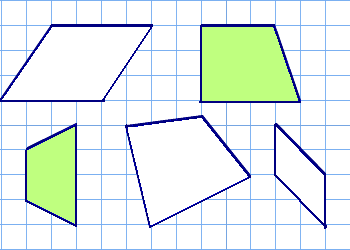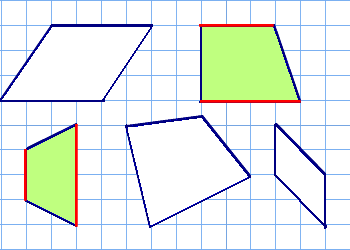



4年算数 垂直 平行と四角形 2 教え方



きれいな鼻は四角形 Part1 三角形を四角形に 美容整形 美容外科のヴェリテクリニック 公式 東京 名古屋 大阪




モデリング カーブツール ポリライン 四角形 頂点と頂点を指定
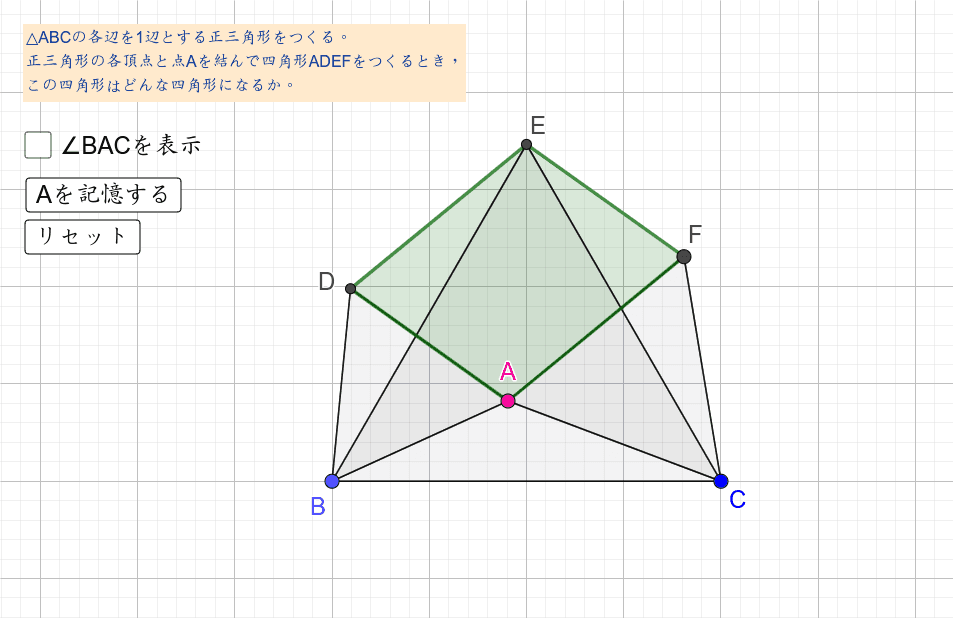



正三角形の頂点がつくる四角形2 Geogebra



角柱の頂点 辺 面の関係 教育考現学



2
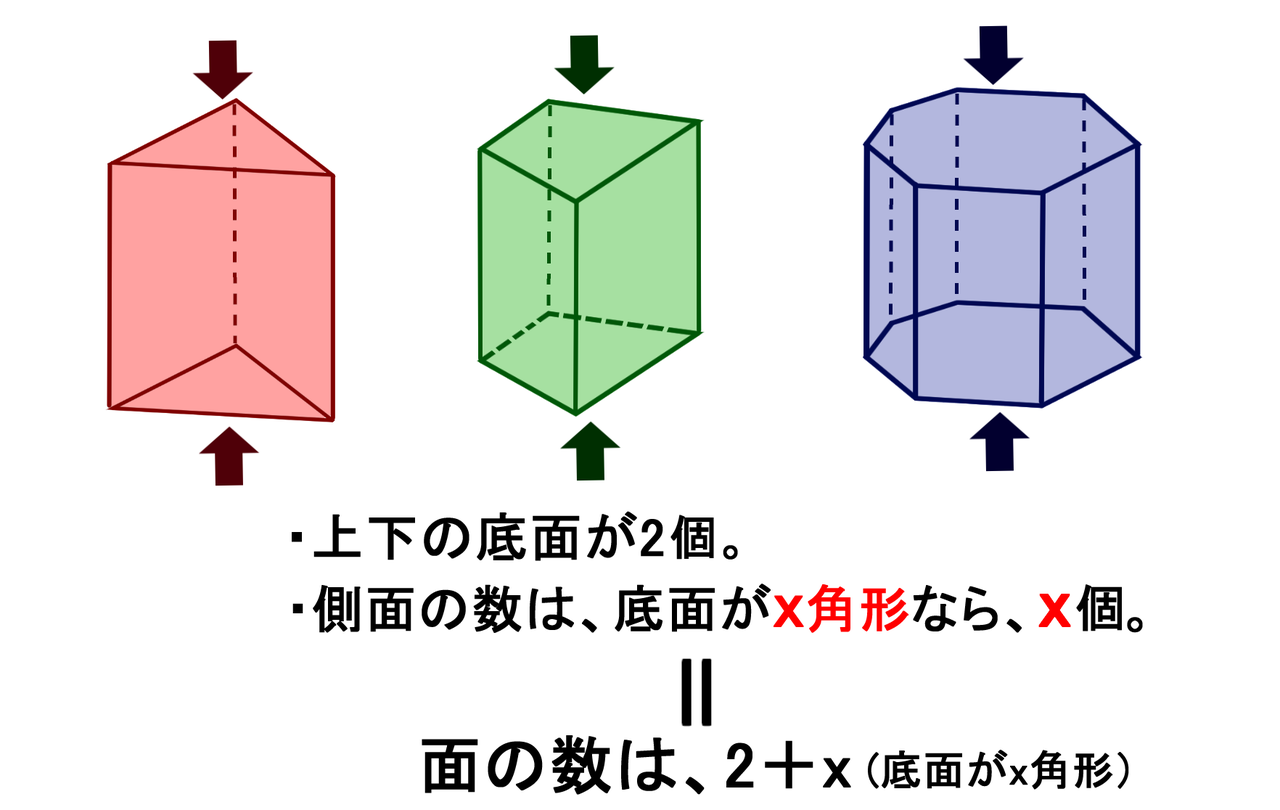



角柱 角錐の辺の数 頂点の数 面の数 バカでもわかる 中学数学




四角形abcdは何通りあるか Accademia Nuts
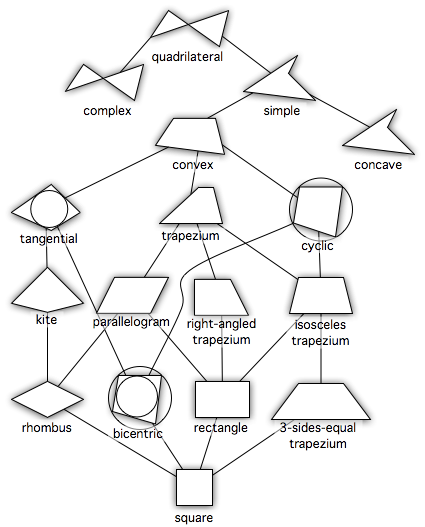



四角形 Wikipedia




オンライン授業 小学校2年生算数 三角形と四角形 辺と頂点 Youtube
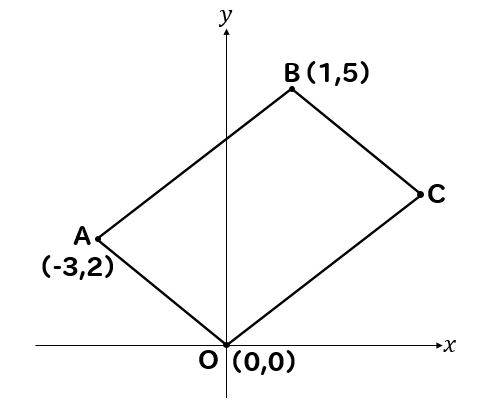



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
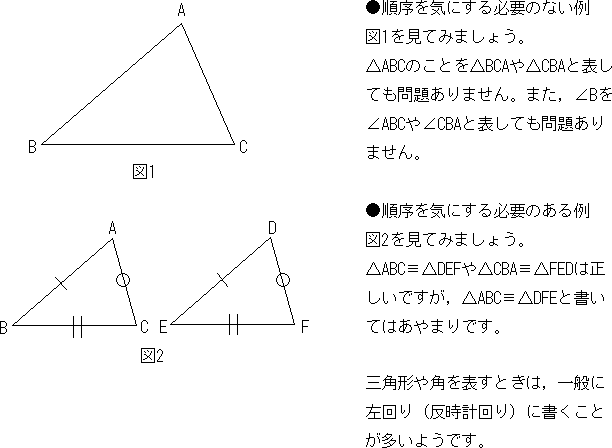



三角形と四角形 角や三角形を表すときの頂点の順序 中学数学 定期テスト対策サイト




四角形の面積を二等分する直線の式 Youtube



四角形から四角形への変換



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材
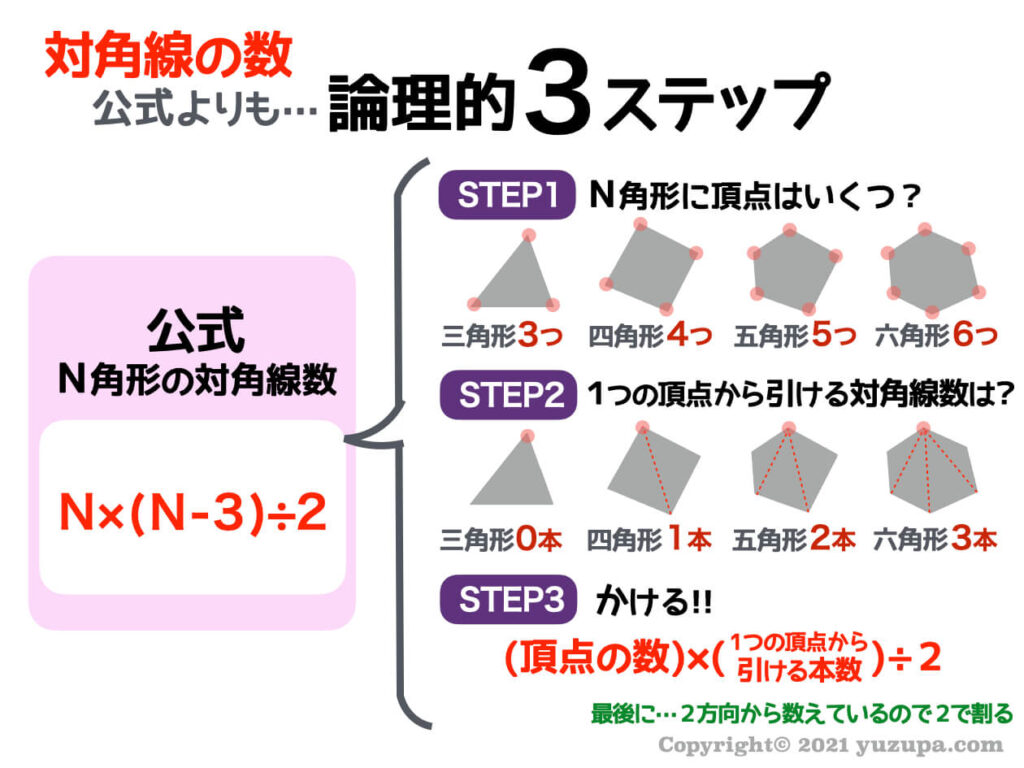



中学受験 対角線の数は 公式を忘れなくする論理的3ステップ かるび勉強部屋
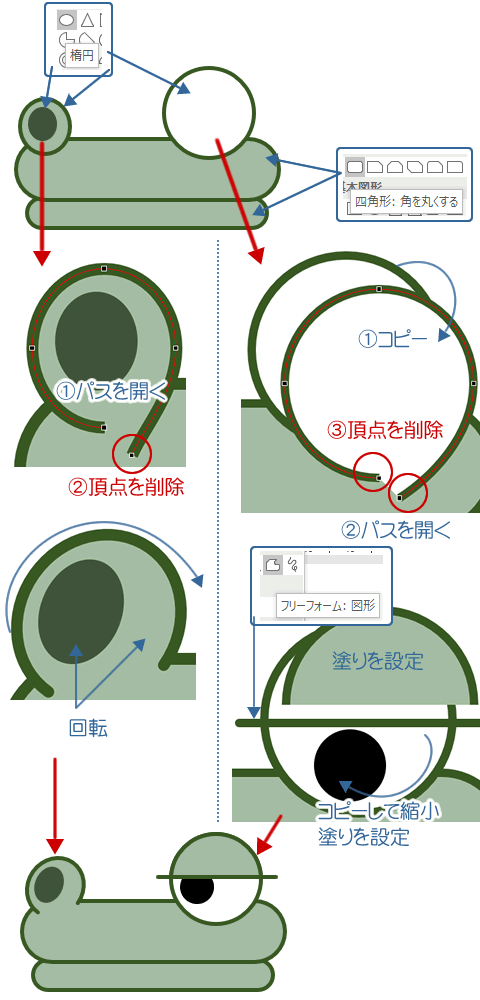



角丸四角形の頂点を利用してワニを描いてみよう Wordあそび
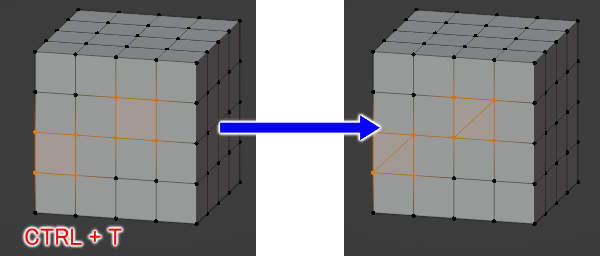



四角形の三角形への分割 メッシュの加工 モデリング 知っておきたい機能 Blender入門 2 8版



1



1
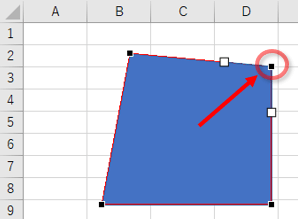



思い通りの図形を作成するための頂点の編集テクニック ノンプログラミングwebアプリ作成ツール Forguncy フォーガンシー グレープシティ株式会社




2 3 どうしてこうなるのかわかりません 答は 2 6 2 3 Clear
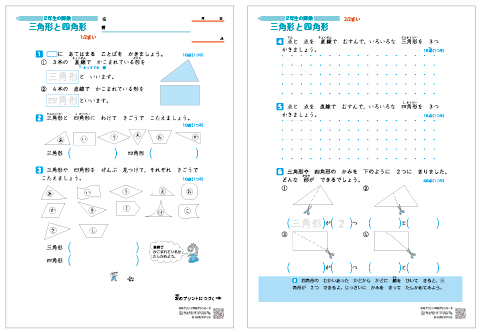



小学2年生の算数 三角形と四角形 直角三角形 正方形 長方形 辺 頂点 直角 練習問題プリント ちびむすドリル 小学生
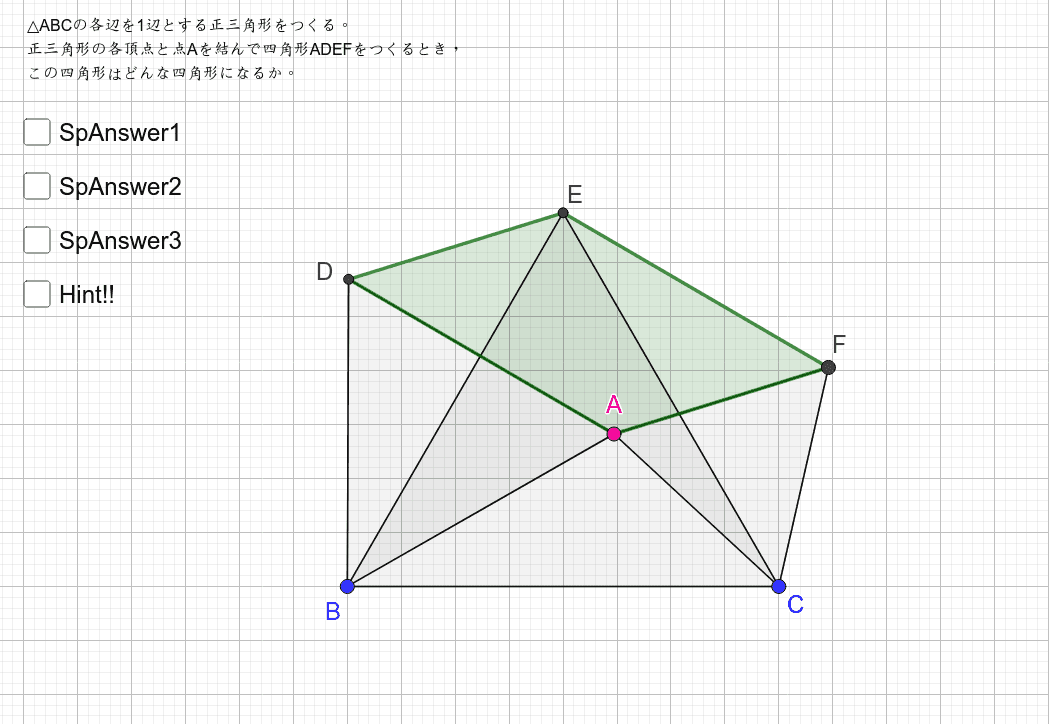



正三角形の頂点がつくる四角形 Geogebra




動点pは四角形abcdの4つの頂点の上を A B C Dの順に進むものとする 高校 教えて Goo



Http Www Edu Tens Net Syohp Murehp Kyuukou Purinto Pridata 6nen 6san6 Pdf




多角形と図形の編集



頂点情報とプリミティブ けんごのお屋敷



四角形から四角形への変換



Www N It Its Jp Uploads B240ddfcba4b17c9d0864e4395bf6b66c9 Pdf



凸四角形



実践記録算数2年



正方形の3等分 Green Artist



Q Tbn And9gctilmsk6n0cugc727 Occs25zacaxldu34x 9vkjwnvuya J Ua Usqp Cau




16 0533号 四角形を補正する補正方法 Astamuse



対応する辺を見つけるには 教育考現学



四角形 Wikipedia



2




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
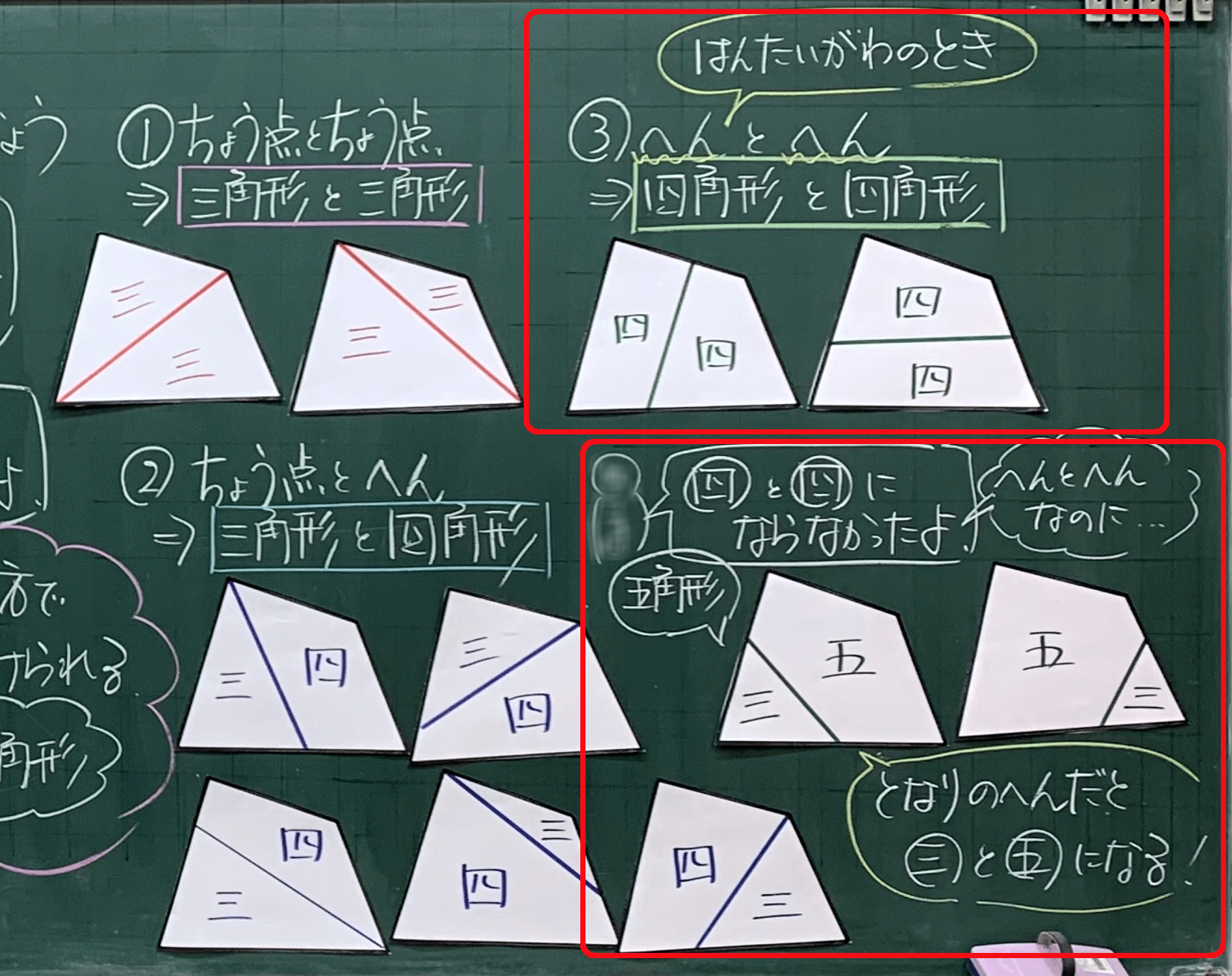



何パターンできるかな 四角形を2つの形に分けまショー 2年 三角形と四角形 4 9時間 板書王のとっておき算数授業 明治図書オンライン 教育zine



4年算数 垂直 平行と四角形 2 教え方



Http Math 005net Com Kaisetu Toseki3 Pdf



対応する頂点 角 辺



2
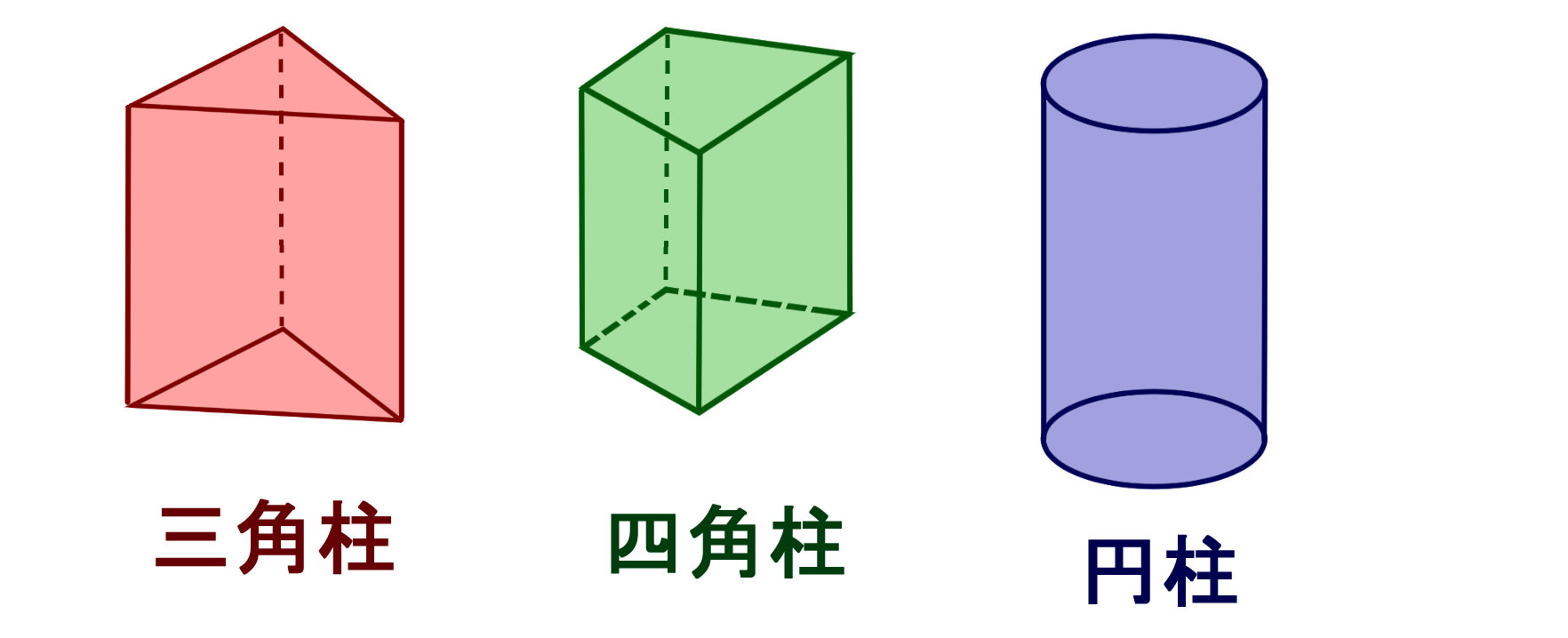



角柱 角錐の辺の数 頂点の数 面の数 バカでもわかる 中学数学
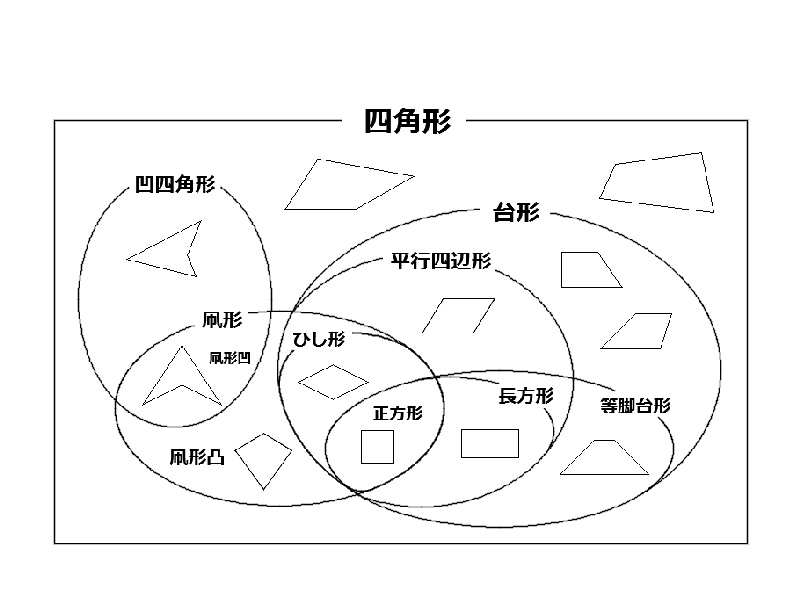



数学 四角形 この世界の勉強記録



横浜女学院11 4 組み合わせ 8個の点から選んで三角形や四角形を作る 気まぐれ解説カフェ 仮




Haruka Aramaki 重なりと連続性 三角形の構成 塗られていない三角形と 塗られている丸と四角で構成している




1994 3458号 四角形の三角形分割装置 Astamuse




二等辺三角形と正三角形 算数用語集




公務員の数的処理の問題でわからないので教えてくださ Okwave




至急 1問でもいいので教えて下さい よろしくお願いします Clear



思い通りの図形を作成するための頂点の編集テクニック ノンプログラミングwebアプリ作成ツール Forguncy フォーガンシー グレープシティ株式会社



0 件のコメント:
コメントを投稿